iO入门03：从MBP开始构建多线性拼图

写在前面

上一期，我们一起看到了【GGH+13】中提出的Multilinear Jigsaw Puzzle大致上是什么个思路。

通过多线性配对这一神奇的工具，我们可以在不知道具体内容的情况下，直接在encoding上“同态计算”多线性配对算法$ e $，最后得到一个在目标group $ \mathbb{G}_T $中的计算结果。

这一工具搭配Barrington‘s Theorem中介绍的矩阵分叉程序（MBP），我们就可以计算未知的MBP程序了。

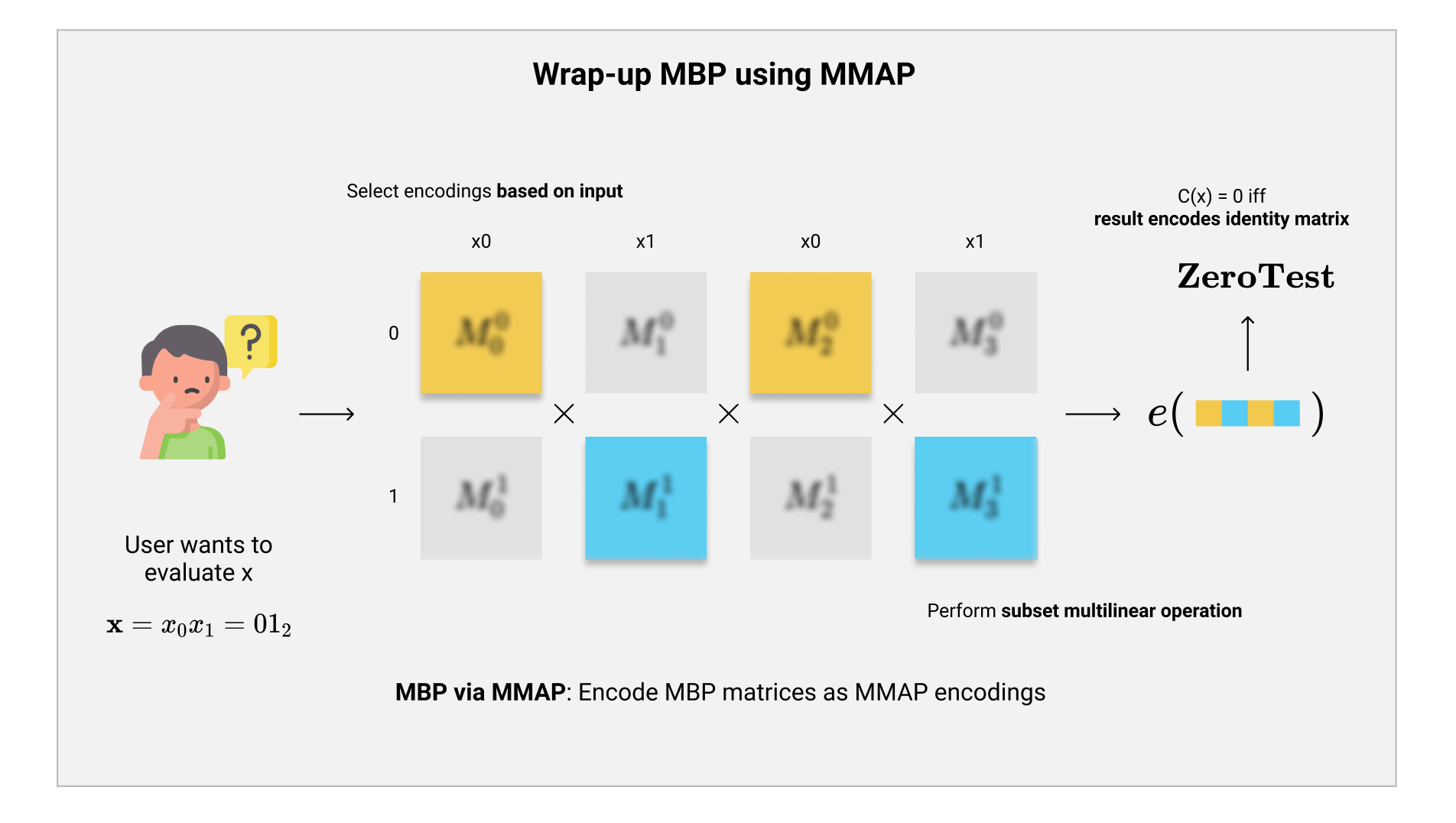
上图是我们上一期结束时所构成的对于$ \mathcal{iO} $的第一次尝试：$ \mathcal{iO}_{MBP} $。大致思路如下：

1. 首先，把我们想要混淆的电路$ C $转换成MBP程序$ P = {\mathbf{inp}(i),\mathbf{M}_{i,b}} $。
2. 随后，我们把这个MBP程序的矩阵部分$ {\mathbf{M}_{i,b}} $encode成多线性配对中的group element，得到$ {\mathbf{g}i^{\mathbf{M}{i,b}}} $。并且我们额外的计算在目标group中的单位矩阵的encoding $ \mathbf{g}_T^{\mathbf{I}_5} $。
3. 最后，我们输出这一系列生成的元素作为电路$ C $的混淆：$ {\mathbf{inp}(i),\mathbf{g}T^{\mathbf{M}{i,b}}}, \mathbf{g}_T^{\mathbf{I}_5} $。

如果我们要计算输入$ x $对应的输出的话，那么我们就选择对应的encoding，根据MBP的计算方法使用Multilinear Map的$ \mathbf{e} $算法来进行矩阵相乘，最后得到在target group中计算结果的encoding。随后，我们在这个结果的encoding中减去$ \mathbf{I}5 $的encoding，就可以使用$ \mathbf{ZeroTest} $来完成计算： $$ C(x) = 0 \iff \mathbf{ZeroTest}(\mathbf{g}T^{\prod \mathbf{M}{i, x{\mathbf{inp}(i)}} - \mathbf{I}_5}) = 0 $$ 在达到正确性（correctness）之后，接下来我们的目标是达到$ \mathcal{iO} $所要求的安全性。

第一个问题：MBP矩阵的不可区分性

我们在上一期结束的时候，已经提到了我们现在的构造$ \mathcal{iO}_{MBP} $的最大问题：因为多线性配对encoding中并不包含randomness，每个encoding都和它的原文保持着紧紧的关联性。

基于这个关联性的攻击显而易见。我们之前举过一个最简单的例子： $$ P_0 := \begin{bmatrix} \mathbf{P} & \mathbf{Q} & \mathbf{P}^{-1} & \mathbf{Q}^{-1}\ \mathbf{I} & \mathbf{I} & \mathbf{I} & \mathbf{I} \end{bmatrix}\ P_1 := \begin{bmatrix} \mathbf{P} & \mathbf{Q} & \mathbf{P}^{-1} & \mathbf{Q}^{-1}\ \mathbf{R} & \mathbf{I} & \mathbf{R}^{-1} & \mathbf{I} \end{bmatrix} $$ $ P_0, P_1 $都是对于AND逻辑门的一个正确的MBP程序，唯一不同的是$ P_0 $的最下面一排矩阵都是单位矩阵$ \mathbf{I} $。因为在indistinguishability的security game当中，Adversary可以任意选择两个功能性完全相等的程序，所以他可以选择$ P_0, P_1 $传给我们的Challenger（挑战者）$ \mathcal{iO}_{MBP} $。

我们的Challenger会根据我们之前定义的步骤，随机选择一个程序，然后输出对应这个程序的8个多线性配对encoding。由于encoding和原文之间的对应关系，所以我们知道，如果原文相同，那么encoding也会相同，反之也是（大概率相同）。所以Adversary就可以直接看返回的encoding中对应MBP程序最下面一排矩阵的4个encoding是否相等，如果相等的话，就知道Challenger选择的是$ P_0 $程序了。

问题的本质：缺少randomness

如果我们仔细的思考这个问题的本质，之所以Adversary可以就算不知道encoding对应的是什么原文的情况下，就可以一下子分辨我们的“混淆”程序对应的到底是哪个程序的原因其实很简单：我们整个encoding系统中没有任何随机性（randomness）的参与。

我们知道，一个加密算法，之所以可以保证语义安全（semantic security，即密文的不可区分性）的原因很简单，因为在加密的时候，我们引进了随机的nonce，所以在Adversary的眼中，两个不同的消息$ m_0, m_1 $的加密$ c_0, c_1 $在概率分布上是基本一致的。

举个最简单的例子来说， AES是一个非常好的对称加密单元，我们可以把它当作一个很安全的PRP（Pseudorandom Permutation，随机排列）来使用。但是光用AES来做加密，即AES-ECB模式，是极其不安全的。AES-ECB模式下的加密就是直接计算$ c = \mathbf{AES}(m) $，这也就是说，如果我们分别加密了两个一样的消息，那么这两个密文会看起来一模一样。光是这个相似的关联性就是致命的。

这就是为什么，我们在使用AES来加密的时候，要正确的使用带有随机nonce的CBC或者CTR模式。简单的来说，就是我们在输入或者输出前会再额外叠加一层随机的mask，用来给密文增加随机性。这样一来我们才可以实现semantic security。

这个问题在我们的$ \mathcal{iO}_{MBP} $中也格为显著。如果我们把多线性配对中的encoding这么个算法当作一个黑盒的话，那其实就和AES-ECB差不多，只起到了一个不可逆的映射的功能，但是对于两个完全相同的矩阵$ \mathbf{M}_0, \mathbf{M}_1 $来说，他们的encoding是一模一样的。

要想解决这个问题，我们就要试图在我们现有的系统中加入randomness。

如何加入Randomness

如果我们想要在整个系统中加入随机性的话，我们最要注意的就是在整个过程中不能破坏原本的功能性/正确性。如果我们就像AES-CBC/CTR一样，直接在原文上XOR随机值的话，那么这些随机化之后的矩阵就会失去原本MBP程序的含义，矩阵相乘的结果也只会是一团乱码。

那么有没有什么方法，可以即保证矩阵相乘的正确性，又可以让每个MBP程序的矩阵都变得随机化，不可区分呢？

要想解决这个问题，我们需要回到1988年。

Kilian Randomization

1988年的时候，计算机科学家Joe Kilian在【Kil88】中做了一件很有意思的事情：基于MBP程序的Two-party MPC。

当时Kilian遇到的问题很简单，如果Alice和Bob想要一起计算一个电路$ C(x) $，其中输入$ x $可以被拆分为$ x_0 \vert x_1 $（我们假设$ x_0, x_1 $分别都是一个bit），其中$ x_0 $为Alice的输入，而$ x_1 $为Bob的输入。目标就是构造一个协议，可以让Bob在不知道Alice的输入是什么的情况下，计算出$ C(x) $的值来。

当时Kilian选择的计算框架，正是来自于Barrington‘s Theorem的MBP框架。在MBP框架中，我们知道对应一个bit的输入就会有若干个对应的矩阵$ \mathbf{M}_{i,b} $，所以我们可以想到一个很简单的toy protocol：

1. 首先，Alice生成一个功能性与电路$ C $相同的MBP程序$ P $，随后她根据自己的输入$ x_0 $选择好对应的矩阵$ {\mathbf{M}_{i, x_0} : \mathbf{inp}(i) = 0} $，随后把这些选择发送给Bob。
2. 随后，Bob通过Oblivious Transfer（OT）协议，从Alice处得到属于自己输入$ x_1 $的MBP矩阵$ {\mathbf{M}_{i, x_0} : \mathbf{inp}(i) = 1} $。如果对于OT不熟悉的话，我们可以大致理解为一个安全的协议，可以让Alice不知道Bob的选择$ b $的情况下，使得Bob获得Alice选择的$ m_0, m_1 $其中的一个消息，而看不到另一个没选择的消息。
3. 最后，Bob把这些矩阵相乘起来，得到MBP程序的运算结果。

当然，细心的朋友们会发现，因为Alice发给Bob的对应了她的选择矩阵是公开的，所以Bob就可以直接通过观察Alice选择的MBP矩阵是什么，反推出Alice的输入$ x_0 $，整个协议并没有实质上的意义。

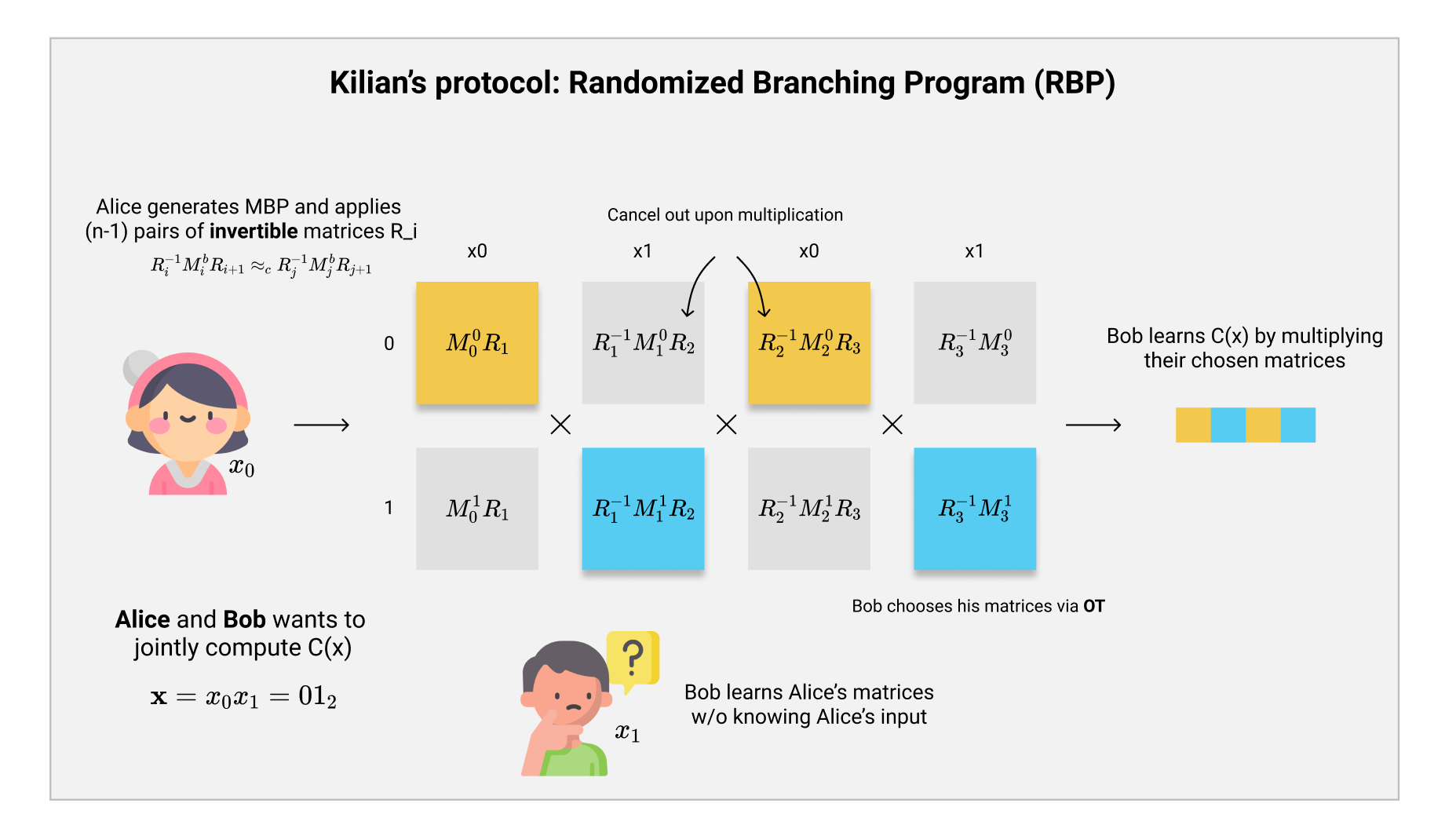
然而，Kilian却找到了一个非常巧妙的方法，解决了这个问题。

Kilian发现，Alice在生成了$ n $对矩阵的MBP程序之后，可以通过一系列巧妙的步骤来“随机化”这个MBP程序。Alice只需要再随机的sample $ n-1 $个$ 5 \times 5 $的纯随机矩阵$ \mathbf{R}_i \in \mathbb{Z}_q $，并且找到他们的inverse $ \mathbf{R}_i^{-1} $。因为矩阵是随机的，所以大概率上是full rank的，反矩阵存在。

获得了$ n-1 $对随机矩阵及其inverse之后，Alice就可以把这些矩阵“叠加”到这$ 2n $对MBP程序矩阵当中，得到随机化的矩阵$ \tilde{\mathbf{M}} $： $$ \tilde{\mathbf{M}}{i, b} = \mathbf{R}i^{-1} \mathbf{M}i^b \mathbf{R}{i+1} $$ 其中，第一组和最后一组矩阵，即$ \mathbf{M}{0, b}, \mathbf{M}{n-1,b} $略微不同，只需要在一边乘上$ \mathbf{R} $矩阵： $$ \tilde{\mathbf{M}}{0, b} = \mathbf{M}0^b \mathbf{R}1\ \tilde{\mathbf{M}}{n-1, b} = \mathbf{R}{n-1}^{-1} \mathbf{M}{n-1}^b $$ 我们很容易就会发现，通过这种方法叠加之后得到的新的$ \tilde{\mathbf{M}} $矩阵仍然保持着MBP程序原有的功能性。如果我们把$ n $个随机MBP矩阵相乘之后，那么每两个矩阵之间的$ \mathbf{R}i, \mathbf{R}i^{-1} $项就会直接相互抵消，最后仍然会得到我们想要的结果： $$ \prod \tilde{\mathbf{M}}{i, x{\mathbf{inp}(i)}} = \prod \mathbf{M}{i, x{\mathbf{inp}(i)}} $$ 实现了功能性之后，我们再来看一下indistinguishability的要求。

通过叠加了$ \mathbf{R} $矩阵之后，原本的MBP矩阵$ \mathbf{M} $其实就被彻底隐藏起来了。因为这$ n $个$ \mathbf{R} $都是随机的，所以任何一组$ \tilde{\mathbf{M}} $矩阵都不会相同，Bob也就没有办法通过看到Alice选择的随机矩阵$ \tilde{\mathbf{M}} $来判断Alice的输入。Kilian在原文中甚至证明了：只要给定任何一个MBP的计算结果$ \Pi $，我们可以完全的模拟（simulate）整个MBP程序中的每个随机矩阵$ \tilde{\mathbf{M}} $！

如果熟悉密码学的安全证明的话，我们就会知道，一旦我们能够证明simulation-based security，那一定就没啥问题了。simulation的要求比起indistinguishability要高得多。

Kilian这里的这个随机化小技巧（Kilian Randomization）生成的随机分布的MBP，我们称之为Randomized Branching Program（RBP）。

使用Kilian Randomization改进$ \mathcal{iO}_{MBP} $

虽然说Kilian原本在【Kil88】中解决的问题是避免Bob通过Alice所选择的MBP矩阵推测出Alice的输入是什么，但是Kilian Randomization这个技巧同样适用于我们这里$ \mathcal{iO}_{MBP} $的问题。

我们会发现，之所以我们描述的攻击是可行的，这是因为encoding没有randomness的成分， 而Kilian Randomization可以给我们的encoding赋予充分的随机性，避免这个问题。

我们修改一下原本的设计，改进成随机化版本的$ \mathcal{iO}_{RBP} $。具体的步骤和之前非常相似，只是在生成MBP程序之后，我们要额外的sample $ n-1 $个随机矩阵$ \mathbf{R} $并计算他们的inverse，随后根据【Kil88】的方法一样叠加到每个$ \mathbf{M} $矩阵上。这样一来，Adversary看到的$ \mathbf{M} $矩阵的encoding $ \mathbf{g}^{\mathbf{M}} $也是随机分布的了。

除此之外，Kilian Randomization还给了我们一个潜在的好处：不允许用户违背MBP程序的规则乱序的矩阵相乘。因为每一个$ \tilde{\mathbf{M}} $矩阵都需要紧跟着下一个矩阵一起才可以把自己身上的randomness $ \mathbf{R} $给抵消掉，所以如果用户违反了这个顺序的话，最后得到的答案一定是一个乱码矩阵，无法从中提取出任何有价值的信息（计算结果）。

看到这里，是不是已经有一种“拼图”的感觉了？我们可以想象着，原本是一盘散落的方块拼图（MBP矩阵），在经过Kilian Randomization之后，逐渐的每个方块上都出现了特有的棱角和花纹（RBP矩阵），并且我们只能按照某种规则把它们排列起来。只不过我们现在拼图上的花纹和棱角还不够明显，仍然可以被巧妙设计的攻击方法所击溃。

下一组问题：违反RBP的计算规则

回顾一下，我们现在的构造$ \mathcal{iO}_{RBP} $，所有的encodings $ \mathbf{g}i^{\tilde{\mathbf{M}}} $都已经加入了一定的randomness，所以直接相互比较的话，是无法从中获得任何与原本的$ \mathbf{M} $矩阵有关的任何信息的。如果我们的Adversary只能够观察（observe）这些随机的矩阵encoding，而不能使用任何计算来进行交互的话，其实$ \mathcal{iO}{RBP} $已经基本具备了不可区分的安全性！

然而，我们都知道，一个合格的Adversary，肯定不会这么简单的放弃。当我们无法从观察这些随机RBP矩阵中得到任何信息的时候，下一步自然而然的，就是通过违反RBP程序计算的规则来寻找漏洞。

之前介绍MBP程序的计算方法的时候，我们都看到了其实我们需要遵守一套较为复杂的规则来得到最终的计算结果，尤其是这两条：

1. 我们需要一路把选出的$ n $个矩阵乘起来，最终得到结果。
2. 我们需要遵守$ \mathbf{inp}(i) $这个mapping，正确的根据输入选择$ \mathbf{M}_{i,b} $矩阵。

我们下面要介绍的两个潜在的attack分别对应上面这两条，这也是【GGH+13】一文中提到的，通过违反了RBP程序的计算规则而实现的attack。

第二个问题：Partial Evaluation Attack（部分乘积攻击）

RBP程序虽然基于MBP程序的基础之上，加入了一系列的randomness $ \mathbf{R} $矩阵，但是这些随机矩阵的分布非常的有规律。

为了保证RBP程序最后的计算结果仍然有效，我们必须要把这些随机的$ \mathbf{R} $矩阵和他们的inverse按顺序放在$ \mathbf{M} $矩阵之间。同时，为了保证不管用户的输入$ x $是什么，最后都可以正确计算，我们必须要确保同一个$ i $下的$ \mathbf{M}{i, 0}, \mathbf{M}{i, 1} $都拥有一样的randomness： $$ \tilde{\mathbf{M}}{i, 0} = \mathbf{R}i^{-1} \mathbf{M}{i, 0} \mathbf{R}{i+1}\ \tilde{\mathbf{M}}{i, 1} = \mathbf{R}i^{-1} \mathbf{M}{i, 1} \mathbf{R}{i+1} $$ 这也就是说，如果原本的$ \mathbf{M}{i, 0}, \mathbf{M}{i, 1} $矩阵都相等，那么加入randomness之后的$ \tilde{\mathbf{M}}{i, 0}, \tilde{\mathbf{M}}{i, 1} $也会是一样的！

基于这一点，我们可以构造出一个特别简单的attack。首先我们选择两个功能完全相等的MBP程序$ P_0, P_1 $： $$ P_0 = \begin{bmatrix} \mathbf{A}&\mathbf{I}\ \mathbf{B}&\mathbf{I} \end{bmatrix}, \mathbf{inp}(0) = 0, \mathbf{inp}(1) = 1\ P_1 = \begin{bmatrix} \mathbf{I}&\mathbf{A}\ \mathbf{I}&\mathbf{B} \end{bmatrix}, \mathbf{inp}(0) = 1, \mathbf{inp}(1) = 0 $$ 其中$ P_0 $的第一列对应第一位输入，第二列对应第二位输入，而$ P_1 $的排列则是反过来的。整个程序的输出（$ \mathbf{A} $或者$ \mathbf{B} $）由第一位输入$ x_0 $所决定。因为这个程序结构的特殊性，MBP矩阵中有一列都是$ \mathbf{I} $矩阵，也就是不管对应的这位bit上的输入，我们选择的矩阵都是相同的。

如果我们把$ P_0 $这个程序转换成RBP矩阵（即加入randomness），我们会得到： $$ \tilde{P_0} = \begin{bmatrix} \mathbf{A}\mathbf{R}_1 & \mathbf{R}_1^{-1}\mathbf{I}\ \mathbf{B}\mathbf{R}_1 & \mathbf{R}_1^{-1}\mathbf{I} \end{bmatrix} $$ 我们会发现，在RBP的形式中，第二列上的两个随机矩阵也是相等的！这也就是说，如果我们输入的MBP矩阵在某一列（即对应某个$ i $）上的两个矩阵是相等的，那么在RBP中这一列上的矩阵也是相等的。在我们举的这个例子中，我们可以很轻易的通过判断混淆之后的RBP矩阵中，哪一列的两个矩阵的encoding相同，来判断混淆的到底是哪个MBP程序。

这一类的攻击，被称之为Partial Evaluation Attack（部分乘积攻击）。一般来说这一类攻击中，Adversary只会计算RBP程序中选出的$ n $个矩阵中$ n’ \le n $个矩阵之间的乘积（我们这里举的例子比较特殊，$ n’ = 1 $）。通俗的来说，Adversary会生成两组不同的输入$ x, x’ $，并且计算： $$ \text{Eval}x = \tilde{\mathbf{M}}{i, x_{\mathbf{inp}(i)}} \tilde{\mathbf{M}}{i + 1, x{\mathbf{inp}(i + 1)}} \dots \tilde{\mathbf{M}}{i + n’, x{\mathbf{inp}(i + n’)}}\ \text{Eval}{x’} = \tilde{\mathbf{M}}{i, x’{\mathbf{inp}(i)}} \tilde{\mathbf{M}}{i + 1, x’{\mathbf{inp}(i + 1)}} \dots \tilde{\mathbf{M}}{i + n’, x’_{\mathbf{inp}(i + n’)}}\ $$ 因为这两条计算链（computation chain）中，不论$ x, x’ $的值是什么，每个位置上的$ \tilde{\mathbf{M}} $矩阵所对应的randomness都是一模一样的，这也就是说，最后输出的结果并不会因为randomness存在而被混淆化。如果在原本的MBP中这两条计算链的输出是相同的，那么在RBP中也是相同的。基于这一点，我们就可以巧妙的选择不同的$ x, x’ $值来，通过观察结果是否相等，不仅可以区分RBP到底是“混淆”了原本的哪个MBP，甚至可以从RBP中提取出原本的MBP出来！

Partial Evaluation Attack的本质

在我们试图修复我们的$ \mathcal{iO}_{RBP} $构造来抵御这一攻击之前，我们不妨来仔细观察一下，为什么Partial Evaluation Attack可以破坏我们构造的安全性。

我们会发现，Kilian Randomization可以确保在不同的$ i $位置上的矩阵之间的不可区分性，但是在相同的$ i $位置上对应0和1的两个矩阵仍然是相同的，并且我们使用不同的输入$ x, x’ $在evaluate整个RBP程序的任意一部分subset的时候，中间的randomness都被抵消，只剩下两侧完全相同的$ \mathbf{R} $矩阵。

这也就是说，之所以这一类的attack可以成功，代表整个系统中的randomness还不够！

之前我们缺少randomness的时候，我们通过了Kilian Randomization的方法来加入一系列随机矩阵，在保持原本功能性的前提下，得到不可区分的RBP矩阵。现在看来，我们得想办法再引进一部分的randomness，以便避免Partial Evaluation Attack。

在加入更多randomness之前，我们心里可能还会有一个疑问：既然整个RBP都是用多线性配对的框架包起来的，是不是只需要增强多线性配对的要求，就可以避免这一类的attack了？

没错，由于我们这里的$ \mathcal{iO} $构造是双层构造，即一个可以计算的里框架（RBP），加上一个可以保证安全性的外框架（多线性配对），所以理论上我们可以在任何一个环节加入新的保护措施（safeguard），使得协议变得安全。但是一般来说，多线性配对的构造都比较脆弱，加入任何一点多的功能都可能会打破功能性和安全性之间的平衡，所以我们如果可以尽量增强里框架的安全性的话，就不要过多的依靠外框架的功能。

综上所述，最好的选择还是使用常规（general）的多线性配对假设，改进我们的内框架，而不修改任何外框架的内容（把多线性配对当作黑盒来使用）。

更多randomness：加入随机维度（High Dimensional Matrices）和挡板（Bookend）

有没有什么方法，可以既加入更多的randomness，使得就算在同一位$ i $上的$ \tilde{\mathbf{M}}{i, 0}, \tilde{\mathbf{M}}{i, 1} $矩阵也完全不相等，但是又不破坏RBP程序本来的功能性呢？

【GGH+13】中，作者把目光方向了扩展矩阵维度这一方案上。

为了使得每个RBP的矩阵都足够随机，我们可以把原本$ 5 \times 5 $的$ \mathbf{M} $矩阵放入一个维度更大的$ \mathbf{D} $矩阵当中。这个$ \mathbf{D} $矩阵的维度为$ 2m + 5 \times 2m + 5 $（稍后会说明$ m $是什么），并且原本的$ \mathbf{M} $矩阵在$ \mathbf{D} $矩阵的右下角。 $$ \mathbf{D}{i, b} = \begin{bmatrix} $&&&\ &\ddots&&\ &&$&\ &&&\mathbf{M}{i,b} \end{bmatrix}\ \tilde{\mathbf{D}}{i, b} = \mathbf{R}i^{-1} \times \begin{bmatrix} $&&&\ &\ddots&&\ &&$&\ &&&\mathbf{M}{i,b} \end{bmatrix} \times \mathbf{R}{i+1} $$ 剩下的$ 2m \times 2m $的左上角部分，我们就会在对角线上填充任意的$ \mathbb{Z}_q $中的随机值。注意这里的随机值是每个$ \mathbf{D} $矩阵都会随机sample的，所以不会存在多个矩阵共享randomness的情况。同理，我们基于新的$ \mathbf{D} $矩阵构造对应的RBP矩阵$ \tilde{\mathbf{D}} $，注意这里我们用到的随机矩阵$ \mathbf{R} $的维度也被放大到了$ 2m + 5 \times 2m + 5 $。

为什么随机值要在对角线上填充呢？这是因为如果放在别的地方，在进行RBP程序运算的时候，随机值的部分可能会干扰到右下角的RBP矩阵相乘结果。

当我们得到这一系列的$ \mathbf{D} $矩阵之后，根据RBP程序的规则把它们按顺序相乘起来的话，那么最后RBP程序的结果就是右下角的$ 5 \times 5 $的方格，而其他地方应该都是我们不需要关心的随机值。但是因为我们目前的计算结果是通过多线性配对的方式来获取的，而多线性配对只能做绝对的$ \mathbf{ZeroTest} $操作，并不能判断哪些是随机值。所以我们需要通过某些手段，把随机的部分去除掉。

解决的方法很简单，我们在计算RBP程序，即做完矩阵相乘之后，我们额外的在两端加上一组挡板向量（Bookend vector）$ \vec{\mathbf{s}}, \vec{\mathbf{t}} $。 $$ \vec{\mathbf{s}} = (\underbrace{0\dots 0}{m \text{ elements}}\ \overbrace{$ \dots $}^{m \text{ elements}}\ \mathbf{s}^*)\ \vec{\mathbf{t}} = (\underbrace{$ \dots $}{m \text{ elements}}\ \overbrace{0 \dots 0}^{m \text{ elements}}\ \mathbf{t}^) $$ 这两个向量的长度均为$ 2m + 5 $。首先，$ \vec{\mathbf{s}} $向量的前$ m $个元素都为0，随后中间$ m $个为$ \mathbb{Z}_q $中sample的随机值，最后5个元素也是随机的，我们用$ \mathbf{s}^ $来表示。$ \vec{\mathbf{t}} $向量构造也类似，只是前面$ 2m $个元素中，0元素的顺序换到了后面。

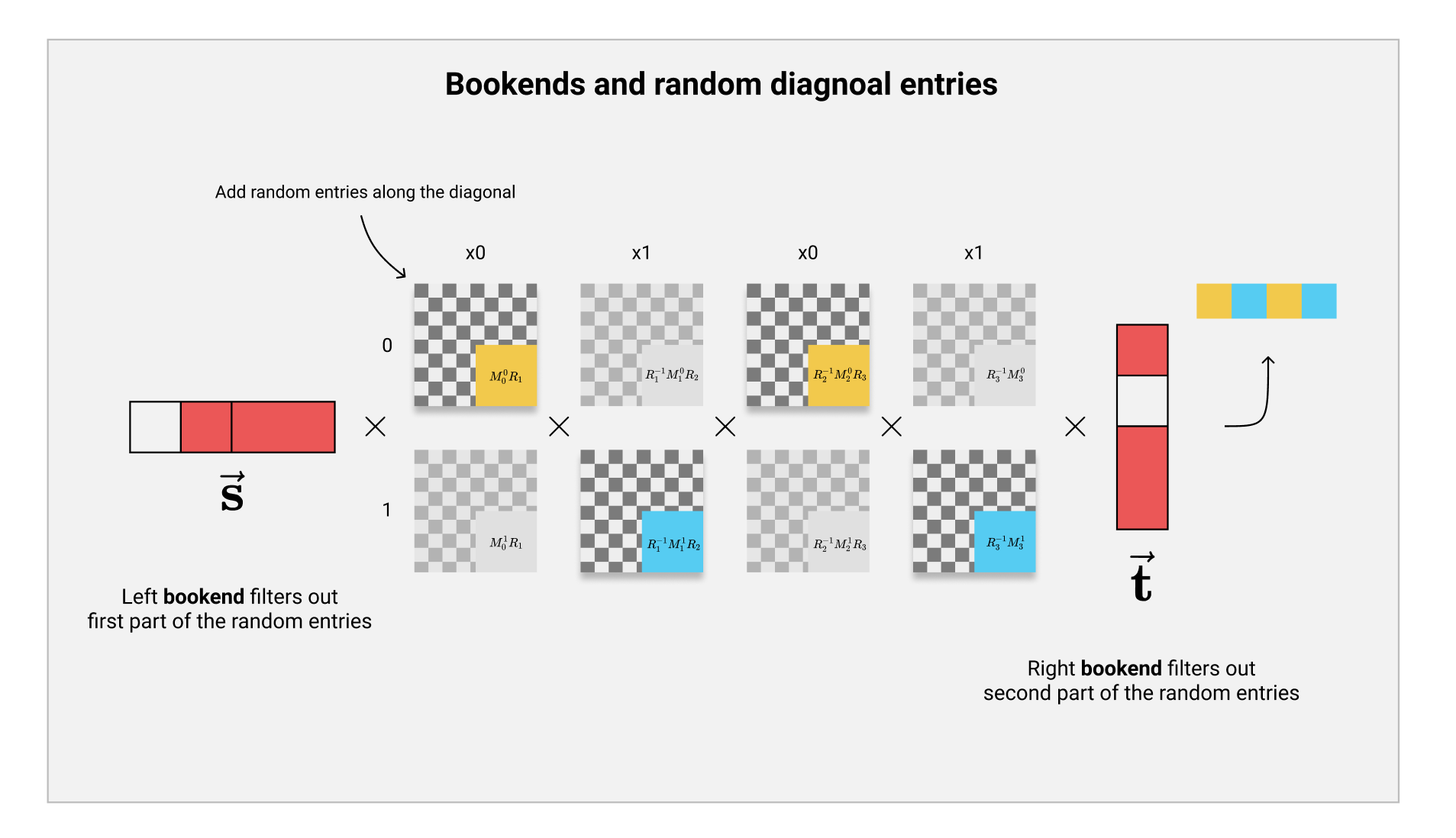
我们基于$ \tilde{\mathbf{D}} $矩阵计算完RBP程序之后，我们可以额外的在最后的结果左右乘上$ \vec{\mathbf{s}} $与$ \vec{\mathbf{t}} $向量： $$ \vec{\mathbf{s}} \cdot \prod \tilde{\mathbf{D}}{i, x{\mathbf{inp}(i)}} \cdot \vec{\mathbf{t}} = \begin{bmatrix} 0&&&\ &\ddots&\ &&0\ &&&\mathbf{s}^* \cdot \prod \mathbf{M}{i, x{\mathbf{inp}(i)}} \cdot \mathbf{t}^* \end{bmatrix}\ $$ 由于这两个向量的特殊构造，就像两个“挡板”一样，巧妙的挡住了我们刚刚加入的随机部分，我们最后就可以得到原来的计算结果了！这两个向量也因此得名，被称作为Bookend vector（挡板向量）。

那么现在我们该如何使用多线性配对来验证计算结果呢？我们观察发现，如果RBP对应的计算结果是0，即最后的$ \prod \mathbf{M}_{i,b} $输出为单位矩阵$ \mathbf{I} $，那么我们这里乘上Bookend之后得到的结果将会是$ \mathbf{p}^* $： $$ \mathbf{p}^* = \begin{bmatrix} 0&&&\ &\ddots&\ &&0\ &&&\mathbf{s}^* \cdot \mathbf{I} \cdot \mathbf{t}^* \end{bmatrix} = \begin{bmatrix} 0&&&\ &\ddots&\ &&0\ &&&\mathbf{s}^* \cdot \mathbf{t}^* \end{bmatrix} $$ 所以，我们只需要把最终计算的结果减去$ \mathbf{p}^* $，就可以使用$ \mathbf{ZeroTest} $来判断RBP的计算结果是否为0了。

此外，因为我们会把挡板向量$ \vec{\mathbf{s}}, \vec{\mathbf{t}} $作为混淆输出的一部分公开，所以我们同样需要使用Kilian Randomization的方法给他们叠加一些randomness，隐藏住它们的结构： $$ \tilde{\vec{\mathbf{s}}} = \vec{\mathbf{s}} \cdot \mathbf{R}0\ \tilde{\vec{\mathbf{t}}} = \mathbf{R}{n}^{-1} \vec{\mathbf{t}} $$ 此外，我们需要更新$ \tilde{\mathbf{D}}{0, b}, \tilde{\mathbf{D}}{n-1, b} $的结构，分别在左右加上$ \mathbf{R}_0^{-1}, \mathbf{R}_n $，保证计算的正确性。

$ \mathcal{iO}_{RBP}^* $的完成态

加上我们刚刚介绍的高维度随机矩阵以及挡板向量之后，我们就从原本的构造进化成了$ \mathcal{iO}_{RBP}^* $，整个系统变得更加强大了。我们在继续后面的讨论之前，不妨先来正式的定义一下现在这个构造的具体结构：

1. 首先，和往常一样，我们生成对应电路$ C $的MBP程序$ {\mathbf{inp}(i), \mathbf{M}_{i, b} : i \in [n], b \in {0, 1}} $。
2. 接着，我们sample $ n + 1 $个随机矩阵$ \mathbf{R}_0, \mathbf{R}_1, \dots, \mathbf{R}_n $，以及它们的inverse。
3. 基于上面生成的$ \mathbf{M} $矩阵，我们首先来构造加入随机维度的$ \mathbf{D} $矩阵。对应每个$ \mathbf{M}{i, b} $，我们把它放在$ 2m + 5 \times 2m + 5 $的$ \mathbf{D}{i, b} $矩阵的右下角，随后在左上角的$ 2m \times 2m $的方块的对角线上填充$ 2m $个$ \mathbb{Z}_q $中生成的随机值。
4. 我们把对应的$ \mathbf{R} $矩阵贴在$ \mathbf{D}{i, b} $的矩阵左右，构成随机化之后的RBP矩阵$ \tilde{\mathbf{D}}{i, b} $：

$$ \tilde{\mathbf{D}}{i, b} = \mathbf{R}i^{-1} \cdot \mathbf{D}{i, b} \cdot \mathbf{R}{i+1} $$

5. 我们根据上面讨论过的要求，生成挡板向量$ \vec{\mathbf{s}}, \vec{\mathbf{t}} $，并且保存这两个向量最后的5个元素为$ \mathbf{s}^, \mathbf{t}^ $。随后我们计算随机化之后的挡板向量$ \tilde{\vec{\mathbf{s}}}, \tilde{\vec{\mathbf{t}}} $：

$$ \tilde{\vec{\mathbf{s}}} = \vec{\mathbf{s}} \cdot \mathbf{R}0\ \tilde{\vec{\mathbf{t}}} = \mathbf{R}{n}^{-1} \vec{\mathbf{t}} $$

6. 最后，我们计算$ {\tilde{\mathbf{D}}{i, b}}, \tilde{\vec{\mathbf{s}}}, \tilde{\vec{\mathbf{t}}}, \mathbf{p}^* \leftarrow \mathbf{s}^* \cdot \mathbf{t}^* $在多线性配对中的encoding $ {\mathbf{g}^{\tilde{\mathbf{D}}{i, b}}}, \mathbf{g}^\tilde{\vec{\mathbf{s}}}, \mathbf{g}^\tilde{\vec{\mathbf{t}}}, \mathbf{g}^{\mathbf{p}^*} $，并且输出我们整个$ \mathcal{iO} $的混淆输出：

$$ \mathcal{iO}{RBP}^* (C) \rightarrow {\mathbf{inp}(i)}, {\mathbf{g}^{\tilde{\mathbf{D}}{i, b}}}, \mathbf{g}^\tilde{\vec{\mathbf{s}}}, \mathbf{g}^\tilde{\vec{\mathbf{t}}}, \mathbf{g}^{\mathbf{p}^*} $$

得到对于电路$ C $的混淆之后，我们在这上面计算输入$ x $的方法也很简单，和之前大致相同：

1. 根据$ \mathbf{inp}(i) $的值以及输入的信息，选取对应的$ \mathbf{D} $矩阵的encoding。
2. 把所有的encoding（以及两侧的挡板向量的encoding）通过多线性配对的方法结合起来，得到计算结果。注意这里我们因为多家了两个encoding，我们需要$ n+2 $阶的多线性配对系统。
3. 最后，我们在目标group的计算结果上减去$ \mathbf{p}^* $对应的encoding，通过$ \mathbf{ZeroTest} $确定计算结果：

$$ C(x) = 0 \iff \mathbf{ZeroTest}(\mathbf{g}^{\tilde{\vec{\mathbf{s}}} \cdot \prod \tilde{\mathbf{D}} \cdot \tilde{\vec{\mathbf{t}}} - \mathbf{p}*}) = yes $$

注意如果我们现在观察任何一个RBP矩阵，或者是试图计算一部分的乘积的话， 因为随机矩阵的存在，并且没有两侧的挡板向量给我们把随机值给去掉的话，我们就没有办法隔着多线性配对来得知任何与MBP矩阵（即电路$ C $）有关的信息。到了这里，我们就成功的修复了我们的$ \mathcal{iO} $构造，可以彻底的抵御Partial Evaluation Attack了！

第三个问题：Input Mixing Attack（乱序输入攻击）

经过第二个问题的考验之后，我们距离最后的成功更进一步了。然而，我们现在面临着一个更大的问题。

我们从一开始讨论MBP程序的工作原理的时候，讲到过除了MBP矩阵相乘之外，另一个格外重要的点在于我们需要根据这个程序特定的$ \mathbf{inp}(i) $这么个mapping，来判断到底在第$ i $个矩阵上，我们需要看输入的那一位来选择。比如说拿我们之前讨论过的AND门的例子来说，因为$ \mathbf{inp}(0) = \mathbf{inp}(2) = 0 $第一对和第三对矩阵，我们都得选择对应$ M_{i, x_0} $的那一个。

一个MBP程序能否成功的生成计算结果，取决于我们是否会严格遵守$ \mathbf{inp}(i) $的这个mapping关系。如果我们一旦不遵守这个mapping，乱序的选择MBP矩阵，不仅我们得不到正确的计算结果，甚至还会暴露出整个MBP程序的具体结构。

MBP程序的这一弱点，正是我们这里$ \mathcal{iO} $构造的大敌。一个Adversary可以通过不遵守$ \mathbf{inp}(i) $ mapping的方法，随意的在任意一位切换0/1的矩阵，然后来推测（probe）出整个MBP矩阵的具体结构！举个比较简单的例子，假如我们的MBP程序在第$ i $对上，一个矩阵为单位矩阵$ \mathbf{I} $，而另一个为一个不是单位矩阵的$ \mathbf{A} $。那么Adversary就可以通过在这一位上来回切换，再验证输出结果的方式，来判断出哪个是$ \mathbf{I} $。更进一步的话，可以结合更多其他位置的矩阵，使用来回切换+验证输出的方式，就可以提取出跟这个MBP程序有关的信息来。

对于这样不遵守$ \mathbf{inp}(i) $的mapping而乱序选择MBP矩阵进行计算的攻击，我们称之为Input Mixing Attack（乱序输入攻击）。

比较遗憾的是，我们之前所增加的两层防护（safeguard），即Kilian Randomization与Bookend，并不能抵挡住乱序输入攻击，这是因为在这种攻击中，Adversary并不会违反MBP程序中矩阵相乘的计算规则，也不会直接去比较encoding之间的区别。

这也就是说，我们还需要增加一种保护措施，强制性的要求所有用户都要遵守$ \mathbf{inp}(i) $所制定的mapping。

分组乘积（Multiplicative Bundling）

Input Mixing Attack的本质其实很简单，我们现在目前所添加的一系列约束仅仅是要求用户得按顺序相乘，并且所有的RBP矩阵得得从头乘到尾，但是并没有要求用户一定得按照某些要求来选择每一对RBP矩阵中的哪一个。

基于这个思路，我们需要添加一个新的约束：对于输入$ x $的任何一位，在计算RBP程序的时候，必须要按照$ \mathbf{inp}(i) $的mapping来完成subset product，如果不按照这个要求就只能得到一堆随机乱码。

具体要怎么做呢？【GGH+13】一文做了一件很聪明的事：遍历一遍$ n $对RBP矩阵，把所有$ \mathbf{inp}(i) $都相等的这些矩阵都单独挑出来，随后在他们身上再添加一些“随机记号”，使得用户在进行计算的时候必须要诚实的根据自己的输入$ x $对应的这一位的值来挑选这些矩阵，这些随机记号才会在计算结束的时候被消除掉。

而这里的“随机记号”，被称作为Bundling Scalars，即分组标量。我们首先在原本的MBP矩阵的基础上，给每个矩阵都乘上一个完全随机的标量（scalar）$ a_{i, b} $： $$ \mathbf{M}{i, b}^* = a{i, b} \mathbf{M}{i,b} $$ 这样一来，我们可以确保任何一个矩阵都拥有一个独一无二的randomness。但是问题显而易见，加上这一组scalars之后，MBP程序原本的功能性就被破坏了。这是因为最后计算的结果将会带上这一组标量的乘积： $$ P{MBP}(x) = \prod a_{i,b} \prod \mathbf{M}{i, x{\mathbf{inp}(i)}} $$ 这样一来，我们原本生成的$ \mathbf{p}^* $就无法帮助我们正确的从结果中抵消掉对应单位矩阵的部分，再使用$ \mathbf{ZeroTest} $来获得结果了。虽然说这样做可以防止乱序输入的方法获得任何有价值的信息，但是让我们想要诚实的计算MBP输出也变得不可能了。这里就是【GGH+13】的闪耀之处：有没有什么方法，可以帮助我们在诚实计算MBP程序的时候，可以完美的抵消掉这一部分随机标量，进而让我们可以通过$ \mathbf{ZeroTest} $来判断计算结果呢？

答案很简单：我们再加入第二组MBP程序，然而这个程序没有任何的功能性，只是一个辅助程序（dummy program）。

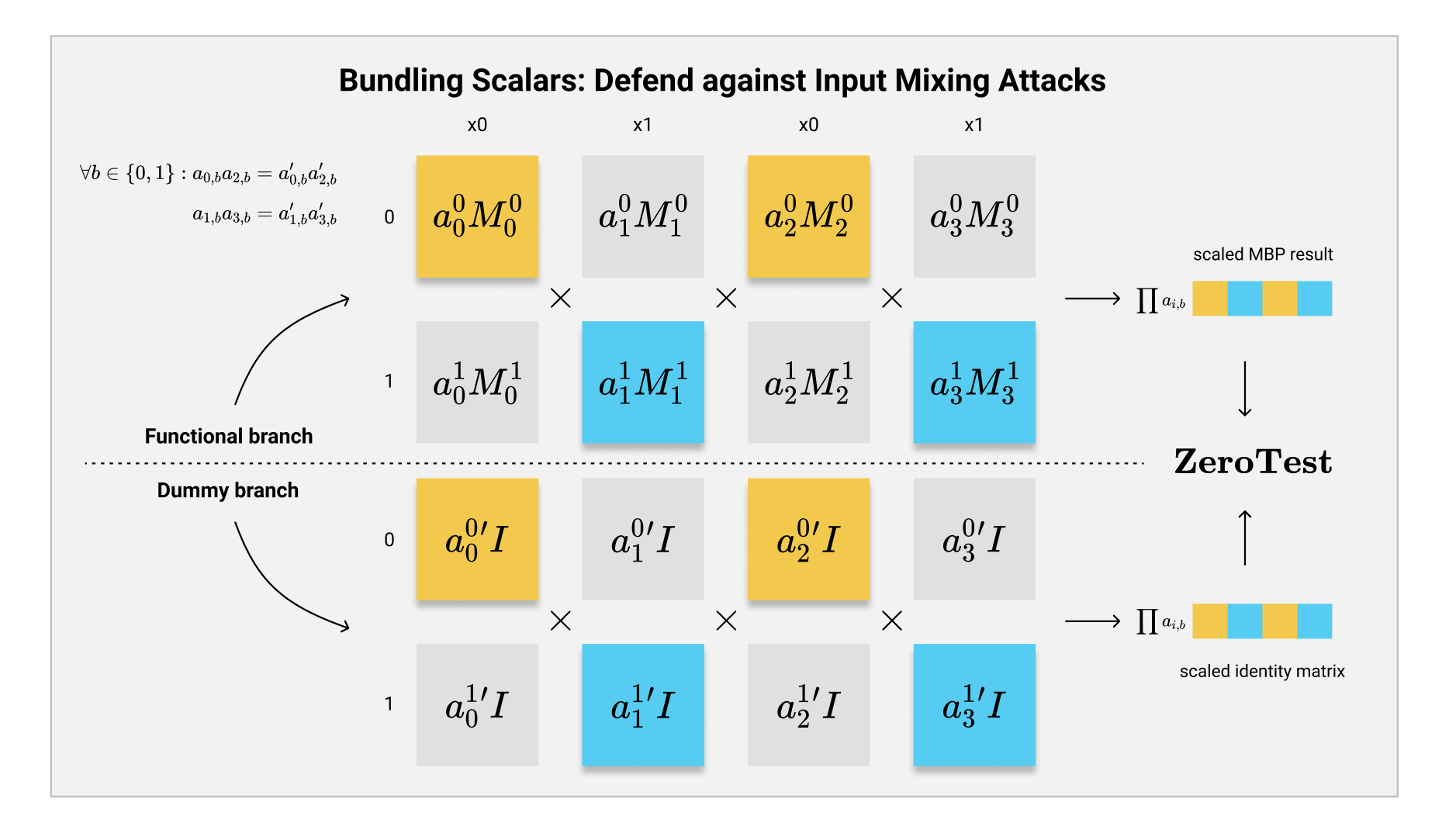
这个辅助程序和原本的MBP程序结构相同，也是由$ 2n $个$ 5 \times 5 $的矩阵构造而成，并且共享$ \mathbf{inp}(i) $的mapping。然而，这个程序中每一个矩阵都是单位矩阵$ \mathbf{I} $，这确保了无论我们输入什么，最后的结果都会是$ \mathbf{I} $。

接下来就是最神奇的思路：我们给这个辅助程序同样添加随机的Bundling Scalars，只是多了一个要求，即对应$ \mathbf{inp}(i) $这一位的，只要用户诚实的按照$ x_{\mathbf{inp}(i)} $的值选择它们，那么这些对应的MBP矩阵中scalars的乘积都和原本的程序相同。

如同上图所示，在这个AND程序中，我们首先会在原本的MBP程序中生成一系列随机的$ {a_{i,b}} $。随后，我们挑选输入的某一位，如$ x_0 $，在所有$ \mathbf{inp}(i) = 0 $的位置所对应的辅助程序的矩阵上，挑选一组新的随机scalars $ a_{i,b}’ $，使得他们的在同一个$ b $值上的乘积相同： $$ \forall j \in \lvert l \rvert, b \in {0,1}: \prod_{\mathbf{inp}(i) = j} a_{i, b} = \prod_{\mathbf{inp}(i) = j} a_{i,b}' $$ 其中，$ l $为输入$ x $的长度。

在上图的这个例子里，我们需要保证在诚实计算的时候，比如$ a_{0, 0} a_{2, 0} $的乘积就与$ a_{0, 0}’ a_{2, 0}’ $的乘积就会相等。但是如果用户乱序计算的话，比如$ x_0 $虽然是0，但是在$ i = 2 $这个位置挑选了代表1的这个矩阵，那么最后$ a_{0, 0} a_{2, 1} $这一组乘积，并不会等于$ a_{0, 0}’ a_{2, 1}’ $，用户也就没法提取出最后的计算结果。

这样一来，只要我们诚实的（不打乱顺序的）根据输入$ x $的每一位的值挑选对应位置的MBP矩阵，同时计算原程序与辅助程序的话，那么最后得到的两个答案就会拥有同样的分组乘积。这个时候，我们就可以通过相减再$ \mathbf{ZeroTest} $的方式来提取出MBP程序的计算结果了。

因为我们需要额外的公开这个辅助程序，我们同样需要给这个程序套上Kilian Randomization和Bookends这两个“保护壳”。为了保证我们不重复使用之前的randomness，我们需要独立的sample随机矩阵$ \mathbf{R}’ $，高维度随机矩阵$ \mathbf{D}’ $，以及挡板向量$ \vec{\mathbf{s}}’, \vec{\mathbf{t}}’ $。

全副武装：【GGH+13】的完全态

讨论了三个潜在的attack以及对应的解决方案之后，我们现在终于达到了【GGH+13】一文中所描述的$ \mathcal{iO}_{RBP}^* $的完全态！我们通过Kilian Randomization防止MBP矩阵泄漏信息，并且保证按顺序相乘。再通过高维度随机矩阵来确保每一对矩阵都不相同，并且通过挡板向量来去掉随机的部分。最后我们使用Bundling Scalars避免Input Mixing Attack，并且再引入了一个辅助程序来使得诚实遵守协议的用户可以正确的判断MBP程序的输出结果。

我们在上期讲到过，这个构造被称作为多线性拼图（Multilinear Jigsaw Puzzle）。我们现在会发现这个名字起的非常贴切，因为我们最后生成的RBP矩阵，加上一系列的safeguard之后，变成了一块块有棱角、形状的拼图块，必须要按照一定的规则才能把它们拼起来得到最后计算的答案。

了解完所有的细节之后，我们来正式的定义完整版的【GGH+13】多线性拼图$ \mathcal{iO}_{MJP} $构造。

首先，我们$ \mathcal{iO} $的输入为一个电路$ C $，我们要求输出的混淆结果在输入电路大小的多项式范围内，即$ \lvert\mathcal{iO}_{MJP}(C)\rvert \le poly(\lvert C \rvert) $。最后，我们的混淆输出需要满足原本的功能性（functionality，或正确性）以及不可区分性（indistinguishability）。

我们具体的构造如下：

1. 根据输入的电路$ C $，使用Barrington‘s Theorem把它转化为一个多项式大小的MBP程序$ {\mathbf{inp}(i), \mathbf{M}_{i,b} : i \in [n], b \in {0,1}} $。
2. 随后，我们根据每个$ i $值，选择一组四个随机的Bundling Scalar $a_{i,0}, a_{i,1}， a_{i,0}’ a_{i,1}’$，并且它们之间满足我们之前描述过的分组乘积相等的要求：

$$ {a_{i,0}, a_{i,1}， a_{i,0}’ a_{i,1}’ : i \in [n]}\ \forall j \in [l] : \prod_{\mathbf{inp}(i) = j} a_{i,0} = \prod_{\mathbf{inp}(i) = j} a_{i,0}’, \prod_{\mathbf{inp}(i) = j} a_{i,1} = \prod_{\mathbf{inp}(i) = j} a_{i,1}' $$

3. 我们使用上述生成的参数，构建一个高维度的随机矩阵$ \mathbf{D}_{i, b} \in \mathbb{Z}q^{2m + 5 \times 2m + 5} $。其中这个矩阵的右下角为加上Bundling Scalars之后的MBP矩阵，而左上角的对角线上则是随机值。我们同时也用同样的方法来构建辅助程序中的$ \mathbf{D}{i, b}’ $矩阵。

$$ \mathbf{D}{i, b} = \begin{bmatrix} $&&&\ &\ddots&&\ &&$&\ &&&a{i, b}\mathbf{M}{i,b} \end{bmatrix}\ \mathbf{D}{i, b}’ = \begin{bmatrix} $&&&\ &\ddots&&\ &&$&\ &&&a_{i, b}’\mathbf{I} \end{bmatrix}\ $$

4. 下一步，我们需要生成挡板向量即Bookends，因为我们有两条计算链，所以我们需要生成两组，即$ \vec{\mathbf{s}}, \vec{\mathbf{t}}, \vec{\mathbf{s}}’, \vec{\mathbf{t}}’ $。此外，我们需要保证这两对Bookends中最后的5个元素之间的内积相等，这样才可以正确完成MBP程序的计算结果验证：

$$ \vec{\mathbf{s}} = (\underbrace{0\dots 0}{m \text{ elements}}\ \overbrace{$ \dots $}^{m \text{ elements}}\ \mathbf{s}^*), \vec{\mathbf{t}} = (\underbrace{$ \dots $}{m \text{ elements}}\ \overbrace{0 \dots 0}^{m \text{ elements}}\ \mathbf{t}^)\ \vec{\mathbf{s}}’ = (\underbrace{0\dots 0}_{m \text{ elements}}\ \overbrace{$ \dots $}^{m \text{ elements}}\ \mathbf{s}^{’}), \vec{\mathbf{t}}’ = (\underbrace{$ \dots $}_{m \text{ elements}}\ \overbrace{0 \dots 0}^{m \text{ elements}}\ \mathbf{t}^{’})\ \langle \mathbf{s}^, \mathbf{t}^* \rangle = \langle \mathbf{s}^{’}, \mathbf{t}^{’} \rangle $$

5. 接下来，我们sample $ 2(n+1) $个随机矩阵，并计算他们的inverse：

$$ {\mathbf{R}_i, \mathbf{R’}_i, \mathbf{R}_i^{-1}, \mathbf{R’}_i^{-1} \in \mathbb{Z}_q^{2m + 5 \times 2m + 5} : i \in [n+1]} $$

6. 最后，我们结合之前生成的所有参数，输出我们的混淆结果$ \mathcal{iO}_{MJP}(C) $：

$$ \mathcal{iO}{MJP}(C) \rightarrow\ {\mathbf{inp}(i) : i \in [n]}, \begin{Bmatrix} \tilde{\vec{\mathbf{s}}} = \vec{\mathbf{s}} \cdot \mathbf{R}0, \tilde{\vec{\mathbf{t}}} = \mathbf{R}n^{-1} \cdot \vec{\mathbf{t}} & \tilde{\vec{\mathbf{s}}}’ = \vec{\mathbf{s}}’ \cdot \mathbf{R’}0, \tilde{\vec{\mathbf{t}}}’ = \mathbf{R’}n^{-1} \cdot \vec{\mathbf{t}}’\ {\tilde{\mathbf{D}}{i, b} = \mathbf{R}{i}^{-1} \mathbf{D}{i,b} \mathbf{R}{i+1} : i \in [n], b \in {0,1}} & {\tilde{\mathbf{D’}}{i, b} = \mathbf{R’}{i}^{-1} \mathbf{D’}{i,b} \mathbf{R’}{i+1} : i \in [n], b \in {0,1}} \end{Bmatrix}\mathbf{g} $$

其中，最右下角的下标$ \mathbf{g} $代表我们花括号中所有的参数都最后输出对应在多线性配对中的encoding。

我们观察发现，我们一共得到了两条随机化之后的RBP计算链条，当我们想要在这个混淆输出上计算任意的输入$ x $的时候，我们只需要：

1. 根据$ \mathbf{inp}(i) $的值，依次的选出对应的两组RBP程序上的矩阵的encoding。
2. 使用多线性配对结合这些encoding，最后得到在目标group中的两个结果的encoding。
3. 最后，相减两个结果，并使用$ \mathbf{ZeroTest} $来判断计算结果：

$$ C(x) = 0 \iff \mathbf{ZeroTest}(\mathbf{g}_T^{\tilde{\vec{\mathbf{s}}} \cdot \prod \tilde{\mathbf{D}} \cdot \tilde{\vec{\mathbf{t}}} - \tilde{\vec{\mathbf{s}}}’ \cdot \prod \tilde{\mathbf{D’}} \cdot \tilde{\vec{\mathbf{t}}}’}) $$

这就是【GGH+13】的完全体了！！感受到这个构造之后，是不是觉得非常优雅，而且没有那么难？这就是密码学的快乐。

写在最后

不知不觉的，这一期的文章又写了一万多字，是时候收尾了。

前两期中，我们从最基础的$ \mathcal{iO} $是什么开始，先探讨了如何选取一个合适的计算框架来表达计算，随后再提出了基于这个框架的一个初步假设。这一期开始，我们基于最初步的$ \mathcal{iO} $构造，深入理解存在的每一种attack以及其背后的本质，随后再对我们的构造加以修补，最后构成了一个完整的多线性拼图系统。

我们对于【GGH+13】的学习就到这里。对于【GGH+13】，还有很多在安全性方面的讨论话题，不过因为篇幅原因，就不多描述啦。

我们会发现，之所以【GGH+13】的构造能够保证不可区分性，一部分是因为我们对于MBP程序的改进，但更多一部分是因为外层的多线性配对框架保证了其安全性。最大的学问也恰好在此。从下期开始，我们来看看【GGH15】这一篇中，究竟如何从最简单的Lattice Problem（即LWE，SIS）开始，构造这么一个强大的多线性配对框架。

下期再见！