格密码学进阶07：GSW同态体系的Key Equation

写在前面

GSW即Gentry-Sahai-Waters全同态加密系统。在我的另一个专题【初探全同态证明】中，已经用了两三篇的篇幅详细介绍过GSW同态加密体系的原理与构造了。

然而在这里，我们重新回顾一下GSW的构造，并且探索一些除了FHE之外，GSW特有的新特性。这些特性对于我们探索后期的应用非常重要。

P.S. 本文主要内容均来自于Hoeteck Wee的一个FHE tutorial，其中用到的图片都来自于原文。

GSW同态加密体系回顾

我们熟悉的FHE（全同态加密）系统，主要的属性分为两点：同态与加密。

其中，同态这一特性为整个系统的功能性（functionality），因为它可以同态的计算密文中的内容，得到新的密文，使得我们完成一定的功能。然而加密这一特性为安全性（security），因为它确保了密文中隐藏的原文不会被提取出来。

我们这里跟随之前类似的视角，先从功能性开始回顾GSW。

Homomorphic Functionality

FHE的functionality属性，如果简单的概括的话，就是我们可以通过$ x $的密文$ ct_x $同态计算某个function $ f $，然后得到： $$ ct_{f(x)} = Eval(pk, ct_x) $$ 其中$ f $可以是任何复杂度与功能性的函数。

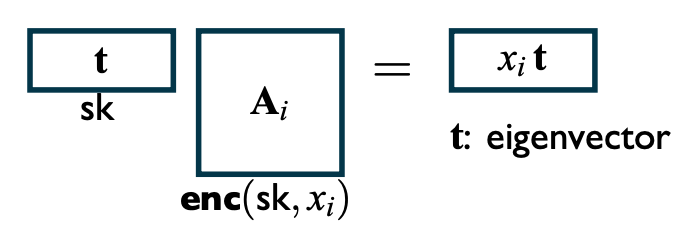
如果只考虑这一特性，我们可以在一开始找到一个很简单的例子：矩阵的特征值（eigenvalue）与特征向量（eigenvector）。

我们假设这个系统中的“密钥”$ sk $是向量$ \mathbf{t} $。假如我们要加密某个值$ x_i $，我们只需要找到一个对应的矩阵$ \mathbf{A}_i $使得： $$ \mathbf{t} \cdot \mathbf{A}_i = x_i \mathbf{t} $$ 这里的$ \mathbf{A}_i $就是密文了。我们可以很简单的发现，我们可以很简单的把不同的$ \mathbf{A}_i $组合起来，同态计算其中的原文： $$ \begin{align*} \text{Add} &: \mathbf{t} \cdot (\mathbf{A}_1 + \mathbf{A}_2) = (x_1 + x_2) \mathbf{t}\ \text{Mult} &: \mathbf{t} \cdot (\mathbf{A}_1\mathbf{A}_2) = x_1x_2 \mathbf{t}\ \text{Polynomial} &: \mathbf{t} \cdot (\mathbf{A}_1\mathbf{A}_2 + \mathbf{A}_3\mathbf{A}_4) = (x_1x_2 + x_3x_4) \mathbf{t} \end{align*} $$ 如果我们总结一下这种表达形式的话，我们可以把要计算的部分用$ f $来代替： $$ \mathbf{t} \cdot \underbrace{f(\mathbf{A}_1, \dots, \mathbf{A}n)}{\mathbf{A}_f} = f(x_1, \dots, x_n) \mathbf{t} $$ 等式的左侧是我们直接通过密文$ \mathbf{A}_i $结合生成的同态计算结果$ \mathbf{A}_f $，而等式的右侧就是直接在原文上计算$ f $的结果。注意在这里，我们使用$ \mathbf{A} $矩阵来表示密文，而不是平常会用到的$ C $，这样的notation和之前稍微不同。

Security

上面给出的构造，虽然实现了functionality，但是完全没有任何security。这是因为给定一个矩阵$ \mathbf{A}_i $，我们可以很轻松的算出他的特征值与特征向量。

所以，第二步我们需要基于原本的构造加入一系列的噪声，使得我们没法通过$ \mathbf{A}_i $推导出$ x_i $。

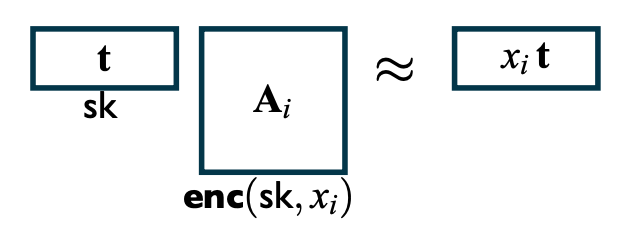
要做的事情很简单，我们只需要在这个等式的左侧加入一定的随机噪声向量，使得原本的相等变成近似相等就可以了。我们这里并不需要过多的了解噪声的构造，只需要大概知道它存在的意义即可。

加上了噪声的这个等式，一下子就变成了格问题中有名的LWE问题。如果我们想要从一个noisy的线性乘积样本中提取出原本的$ \mathbf{t} $，这个问题被公认是困难的。

接下来，我们快速的sanity check一下之前的同态特性。

首先，同态计算加法仍然是可行的： $$ \mathbf{t} \cdot (\mathbf{A}_1 + \mathbf{A}_2) \approx (x_1 + x_2) \mathbf{t} $$ 这是因为虽然$ \mathbf{A}_1, \mathbf{A}_2 $中都带有一定的噪声，但是这些噪声都是有限的（small）。所以small + small = small，我们得到的结果也是一个有限噪声的密文。

然而，同态乘法计算不行了： $$ \mathbf{t} \cdot (\mathbf{A}_1 \mathbf{A}_2) \not\approx x_1x_2 \mathbf{t} $$ 这是因为，当我们相乘$ \mathbf{A}_1 $与$ \mathbf{A}_2 $的时候，我们变相的在把$ \mathbf{A}_1 $中的噪声项乘以$ \mathbf{A}_2 $本身。因为$ \mathbf{A}_2 $并不是有限分布（small）的，所以最后得到的结果的噪声会变的不可控制。

Make $ \mathbf{A}_i $ small

即然之前乘法失败的原因是因为$ \mathbf{A}_2 $的分布不是small的，那么假如我们把所有的$ \mathbf{A}_i $矩阵都可以变成small的，那么问题就解决了。这样的话，我们就可以在噪声范围的允许下，同态的计算任意的函数$ f $： $$ \mathbf{t} \cdot \underbrace{f(\mathbf{A}_1, \dots, \mathbf{A}n)}{\mathbf{A}_f} \approx f(x_1, \dots, x_n) \mathbf{t} $$

构建GSW等式

回顾完了GSW的大致原理之后，接下来我们来看GSW在Lattice中的具体构造。

首先，我们要把要用到的LWE问题（近似特征向量）设置好。我们选择一个随机的矩阵$ \mathbf{B} $，以及一个随机的向量$ \mathbf{s} $，还有small的噪音$ \mathbf{e} $。我们可以把这三个元素组合起来，变成我们预期的大概结构： $$ \underbrace{\begin{pmatrix}\mathbf{s} & -1 \end{pmatrix}}_{\mathbf{t}} \cdot \begin{pmatrix}\mathbf{B}\ \mathbf{sB + e}\end{pmatrix} \approx 0 $$ 这里左侧的向量$ (\mathbf{s}\ -1) $就是我们之前所提到的$ \mathbf{t} $向量（即密钥）了。

随后，我们往等式中加入要加密的原文$ x $： $$ \underbrace{\begin{pmatrix}\mathbf{s} & -1 \end{pmatrix}}{\mathbf{t}} \cdot \underbrace{\left( \begin{pmatrix}\mathbf{B}\ \mathbf{sB + e}\end{pmatrix} + x \mathbf{I} \right)}{\mathbf{A}} \approx x \mathbf{t} $$ 我们注意这里的乘法右侧，就是我们的$ \mathbf{A} $矩阵（即密文）了。因为DLWE的难度告诉我们，$ \begin{pmatrix}\mathbf{B}\ \mathbf{sB + e}\end{pmatrix} $的概率分布与一个纯平均分布的随机矩阵难以辨别，所以我们可以把这一部分作为一个OTP，遮盖住里面的原文$ x \mathbf{I} $。

二进制分解$ \mathbf{A} $

接下来，和我们之前说的一样，我们需要把$ \mathbf{A} $矩阵的取值范围变小到二进制$ {0, 1} $。这样一来，就可以满足我们之前提到的同态乘法的噪声分布要求。

为了能够把一个矩阵或者向量变成二进制态，我们需要引入一个二进制分解函数$ \mathbf{G}^{-1} $。这在介绍GSW的文章中我们详细描述过了，在这里就一笔带过。$ \mathbf{G}^{-1} $还对应着一个二进制的重组矩阵$ \mathbf{G} $，并且满足了$ \mathbf{G} \cdot \mathbf{G}^{-1}(\mathbf{M}) = \mathbf{M} $的属性。

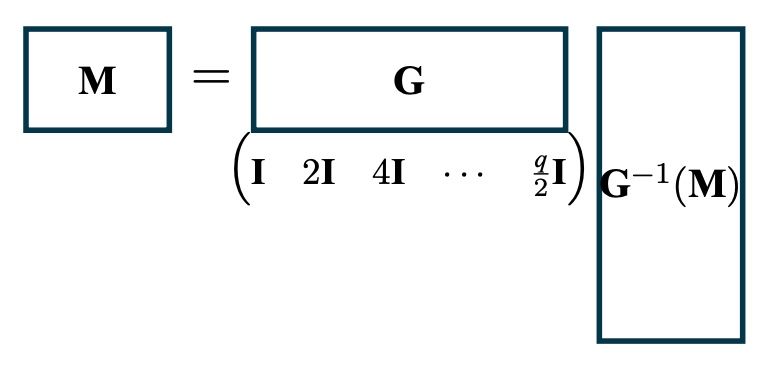
注意这里的$ \mathbf{G} $是一个矩阵。这也就代表了，二进制分解虽然很复杂（是一个函数），而重组回十进制只需要一个很简单的线性变换（即矩阵相乘）就可以做到。

接下来，我们引入$ \mathbf{G} $与$ \mathbf{G}^{-1} $，试图修改一下原本的等式： $$ \overbrace{\underbrace{\begin{pmatrix}\mathbf{s} & -1 \end{pmatrix}}{\mathbf{t}} \mathbf{G}}^{\mathbf{t}’} \cdot \underbrace{\mathbf{G}^{-1}\left( \begin{pmatrix}\mathbf{B}\ \mathbf{sB + e}\end{pmatrix} + x \mathbf{I} \right)}{\mathbf{A}} \approx x \mathbf{t} $$ 这样一来，我们发现原本的$ \mathbf{A} $矩阵被二进制分解了，所以每一个值都只能是0和1，满足了我们之前的要求。为了使得整个等式仍然成立，我们需要加入一个$ \mathbf{G} $矩阵来重组分解之后的$ \mathbf{A} $。

因为原本的等式中额外加入了两项，我们接下来需要重新的调整一下$ \mathbf{t} $与$ \mathbf{A} $的定义，使得整个等式仍然保持一个$ \mathbf{t} \cdot \mathbf{A} \approx x \mathbf{t} $的构造。在等式中，我们已经标注出了新的$ \mathbf{t}’ $向量，即$\begin{pmatrix}\mathbf{s} & -1 \end{pmatrix}\mathbf{G}$。

随后，我们需要更新$ \mathbf{A} $矩阵中的表达式，使得基于$ \mathbf{t}’ $的等式成立： $$ \overbrace{\underbrace{\begin{pmatrix}\mathbf{s} & -1 \end{pmatrix}}{\mathbf{t}} \mathbf{G}}^{\mathbf{t}’} \cdot \underbrace{\mathbf{G}^{-1}\left( \begin{pmatrix}\mathbf{B}\ \mathbf{sB + e}\end{pmatrix} + x \mathbf{G} \right)}{\mathbf{A}} \approx x \mathbf{tG} = x \mathbf{t}' $$ 我们最后得到的这个等式，就是GSW加密系统的全貌啦。虽然看起来复杂，但是我们只需要记得最简单的表达形式就足够了： $$ \mathbf{t} \cdot \mathbf{A} \approx x \mathbf{t} $$

GSW中的噪声增长

接下来，我们来看一下GSW中进行同态计算时的噪声增长规律。

密文相乘的奥秘

当我们相乘两个密文$ \mathbf{A}_1, \mathbf{A}_2 $的时候，我们有两种相乘的方法， 都可以符合之前定义的“small”。

第一种相乘的方法，是把$ \mathbf{A}_1, \mathbf{A}_2 $全部进行二进制分解，然后再相乘，即： $$ \mathbf{G}^{-1}(\mathbf{A}_1) \cdot \mathbf{G}^{-1}(\mathbf{A}_2) $$ 这样一来，等于我们是在相乘两个二进制矩阵。假如每个密文一开始的噪声level都是“small”，我们用这种方式同态计算$ f $之后，得到的噪声增长趋势则为： $$ small^{\deg(f)} $$ 这里$ \deg (f) $为$ f $函数的degree，即乘法计算的次数。

第二种相乘的方法则不太一样，因为GSW的乘法计算是不对称的（我们只需要考虑$ \mathbf{A}_2 $的大小），所以我们只二进制分解后面的，然后在进行下次计算前，再把密文分解一次： $$ \mathbf{G}^{-1}(\mathbf{A}_1 \cdot \mathbf{G}^{-1}(\mathbf{A}_2)) $$ 这样的话，我们等于是进行了一次噪声与small的相乘之后，然后再分解了一次，把噪声的分布又压回了small。这种方式下的噪声增长趋势为： $$ small^{\log \deg(f)} $$ 我们发现第二种方法结合密文可以让噪声的增速减少很多！

总结一下，当我们同态的计算密文的乘法的时候，比起把所有的密文都二进制分解了乘在一起，我们更应该依次计算，先分解一个，乘一次，然后再分解一次。这样更能控制住噪声的增幅，从而决定了modulus的大小。

同态计算方案的区别

同样的FHE系统，计算同样的$ f $功能，却能带来完全不同的噪声增长。这是因为计算方案不同所导致的。

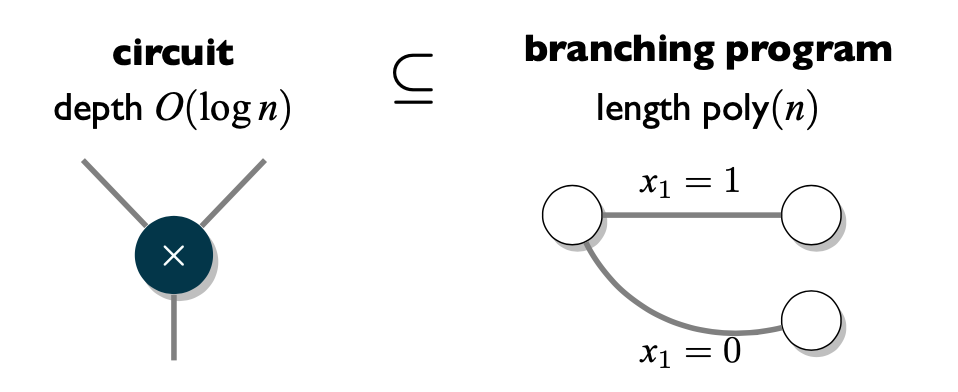
假如我们要同态的计算一个function $ f $，其实有两种最常见的方案来实现它。

第一种方案是最intuitive的方案，即用电路（arithmetic circuit）来表达$ f $，然后再用我们之前看到的加法与乘法的计算方法来同态计算它。

然而电路带来的问题是，它是由各个逻辑门（gate）组成的。当我们提供输入之后，这些输入就会不断的在各个gate中计算，然后结果再流进下个gate进行下一步计算，组成一个gate的串联结构。这样就带来了一个问题：因为每一个gate都会变相的增大密文中的噪声，我们越往后的gate，所看到的输入的噪声就越来越大，然后在进行乘法的时候增加的噪声也会随之增大（因为噪声项也会影响乘积）。这个问题的根本原因在于电路本身的特性：我们不断的组合intermediate的计算结果（即计算到一半的结果）来生成最后的结果。假如我们拥有一个$ O(\log{n}) $大小的电路，那么同态计算之后的结果的噪声也会是exponentially增长的，大概为： $$ noise_{output} = n^{O(\log{n})} \cdot noise_{input} $$ 然而，我们计算一个“程序”，其实还有第二种方法，即把它转换为一个Matrix Branching Program（MBP）。这在上一篇文章中有所提到，根据Barrington‘s Theorem【Bar86】，一个$ \mathbf{NC}_1 $的电路，即深度在$ O(\log{n}) $的电路，可以被转换成一个多项式大小的MBP。这个MBP的长度为即$ poly(n) $。

MBP不同于电路的一个属性在于，我们计算一个程序是通过输入来“选择”一系列的矩阵相乘起来。因为我们选择的这些矩阵都是全新的（未被同态计算过的），所以等于是我们会相乘一系列freshly encrypted的密文。这一点确保了我们不会相乘两个噪声增长都很大的intermediate steps在一起，导致噪声更快的增长。所以如果我们基于MBP形式同态计算相同的程序$ f $的话，我们的噪声增长会是线性的，大概为： $$ noise_{output} = n \cdot poly(n) \cdot noise_{input} $$ 注意这里我们是大概的约束了一下噪音增长的幅度，并没有仔细的分析具体的噪声的展开式。不过通过初步的分析，已经可以看出来，GSW FHE在进行同态计算的时候，因为乘法计算中噪声增长的asymmetry，我们可以巧妙的利用同一个程序的不同形态（即MBP）来最大程度额抑制噪声增长。

当我们使用MBP来进行同态计算之后，因为噪声的增长和电路的深度是多项式关系，所以我们选取的LWE modulus $ q $和噪声范围$ B $也是多项式关系。对于这种参数关系的LWE问题的难度，我们称之为polynomial hardness。

GSW的Key Equation

接下来，是这一篇文章最重要的部分，我们要基于之前给出的GSW加密关系式$ \mathbf{t} \cdot \mathbf{A} \approx x \mathbf{t} $，推导出GSW中最具有代表性意义的Key Equation。

Eigenvector系统的关键等式

我们在这篇文章的最初提到了最简单的“FHE”，使用一个矩阵Eigenvector的属性构造的体系。这个体系只实现了Functionality，但是没有实现Security。我们在推到GSW的关键等式之前，不妨再重新看一下基于Eigenvector的这一构造。

首先，基于Eigenvector的特性，我们知道这个系统的正确性，即“密文”可以被成功还原为原文： $$ \mathbf{t} \cdot \mathbf{A}_i = x_i \mathbf{t} $$ 我们重新变换一下这个等式，把所有含有$ \mathbf{t} $的部分挪到左边： $$ \mathbf{t} \cdot (\mathbf{A}_i - x_i \mathbf{I}) = 0 $$ 为了使得$ x_i $项的维度符合等式，我们把$ x_i $这一项乘上了identity matrix $ \mathbf{I} $矩阵。

同理可得，我们可以基于这一等式，推导出同态计算之后的结果的正确性： $$ \mathbf{t} \cdot (\mathbf{A}_i - x_i \mathbf{I}) = 0 \implies \mathbf{t} \cdot (\mathbf{A}_f - f(x) \mathbf{I}) = 0 $$ 我们把这一组等式，标注为Lemma I。

随后，基于这个体系，我们还可以得到一个更加广泛的Lemma II，并且其中包含了Lemma I中的内容。

Lemma II指出，给定任意的密文矩阵$ \mathbf{A}i $，与任意的加密原文$ x $和同态计算的函数$ f $，我们都可以找到一个对应的矩阵$ \mathbf{H}{f,x} $，使得可以满足： $$ \forall \mathbf{A}i, \forall x, \forall f, \exists \mathbf{H}{f,x}:\ [\mathbf{A}_1 - x_1 \mathbf{I} \vert \cdots \vert \mathbf{A}n - x_n \mathbf{I}] \cdot \mathbf{H}{f,x} = \mathbf{A}_f - f(x) \mathbf{I} $$ 我们观察发现，Lemma II直接包含了Lemma I的内容。我们可以在等式的两侧都乘上$ \mathbf{t} $： $$ \mathbf{t} \cdot [\mathbf{A}_1 - x_1 \mathbf{I} \vert \cdots \vert \mathbf{A}n - x_n \mathbf{I}] \cdot \mathbf{H}{f,x} = \mathbf{t} \cdot (\mathbf{A}_f - f(x) \mathbf{I}) $$ 根据我们之前的得到的等式，我们会发现左侧的$ \mathbf{t} $乘上整个矩阵都会等于0。相同的，在右侧的$ \mathbf{t} $乘上对应的矩阵也会等于0，所以等式成立。

Eigenvector体系的关键等式证明

接下来，我们就需要证明，在我们之前看到的加法和乘法的例子中，我们真的可以找到这样的$ \mathbf{H}_{f,x} $矩阵，满足这一等式。

首先来看加法。假如我们拥有$ \mathbf{A}_1, \mathbf{A}2 $这两个矩阵，我们计算加法的方式就是把他们相加起来。对应的，我们也可以找到$ \mathbf{H}{+, x_1, x_2} $矩阵： $$ [\mathbf{A}1 - x_1 \mathbf{I} \vert \mathbf{A}2 - x_2 \mathbf{I}] \cdot \underbrace{\begin{pmatrix}\mathbf{I}\ \mathbf{I} \end{pmatrix}}{\mathbf{H}{+, x_1, x_2}} = \underbrace{(\mathbf{A}1 + \mathbf{A}2)}{\mathbf{A}+} - (x_1 + x_2) \mathbf{I} $$ 其次，我们来看乘法。同样，假如我们计算$ \mathbf{A}_1, \mathbf{A}2 $的同态乘法，那么我们直接把他们相乘起来即可。对应的$ \mathbf{H}{\times, x_1, x_2} $也很简单： $$ [\mathbf{A}_1 - x_1 \mathbf{I} \vert \mathbf{A}2 - x_2 \mathbf{I}] \cdot \underbrace{\begin{pmatrix}\mathbf{A}2\ x_1\mathbf{I} \end{pmatrix}}{\mathbf{H}{\times, x_1, x_2}} = \underbrace{\mathbf{A}1 \mathbf{A}2}{\mathbf{A}\times} - x_1x_2 \mathbf{I} $$ 因为我们找到了乘法和加法对应的$ \mathbf{H} $矩阵，所以我们可以把这两个矩阵根据实际要计算的电路构造组合起来，构成进行任意计算的$ \mathbf{H} $矩阵了。

Q.E.D.

从Eigenvector体系过渡到GSW

接下来，我们开始尝试推到最关键的等式，即代表GSW的Key Equation。

由于之前我们都是在特征向量体系上推到的，现在我们需要把它转换成近似特征向量体系（即GSW）。换句话来说，我们需要在这个系统中把原本的一部分等式变成近似等式，然后把$ \mathbf{I} $矩阵替换为$ \mathbf{G} $矩阵。

我们首先改变Lemma I中的最初等式： $$ \mathbf{t} \cdot \mathbf{A}_i \approx x_i \mathbf{t} \cdot \mathbf{G} $$ 同理可得，我们可以推导出同态计算之后的等式： $$ \mathbf{t} \cdot \mathbf{A}_f \approx f(x) \mathbf{t} \cdot \mathbf{G} $$ 如果转换成上述Lemma I中的格式，那我们可以得到： $$ \mathbf{t} \cdot (\mathbf{A}_i - x_i \mathbf{G}) \approx 0 \implies \mathbf{t} \cdot (\mathbf{A}f - f(x) \mathbf{G}) \approx 0 $$ 接下来，我们改变Lemma II。我们这里除了需要把$ \mathbf{I} $矩阵替换成$ \mathbf{G} $之外，还需要额外的约束$ \mathbf{H}{f,x} $是一个短矩阵，取值范围为“small”： $$ \forall \mathbf{A}i, \forall x, \forall f, \exists \text{ small } \mathbf{H}{f,x}:\ [\mathbf{A}_1 - x_1 \mathbf{G} \vert \cdots \vert \mathbf{A}n - x_n \mathbf{G}] \cdot \mathbf{H}{f,x} = \mathbf{A}_f - f(x) \mathbf{G} $$ 为什么$ \mathbf{H} $矩阵需要是短的呢？这是因为我们需要约束它来控制噪声的增长范围。我们可以同样的在等式的两侧乘上$ \mathbf{t} $： $$ \mathbf{t} \cdot [\mathbf{A}_1 - x_1 \mathbf{G} \vert \cdots \vert \mathbf{A}n - x_n \mathbf{G}] \cdot \mathbf{H}{f,x} = \mathbf{t} \cdot (\mathbf{A}_f - f(x) \mathbf{G}) $$ 因为根据修改过后的Lemma I，我们知道$ \mathbf{t} $乘以$ \mathbf{A}_i - x_i \mathbf{G} $之后会得到一个近似于0的结果（即噪声）。所以在这里我们等式的左侧和右侧都会得到一个$ \approx 0 $的噪声。为了使得等式成立，我们不得不选择一个短的$ \mathbf{H} $矩阵，使得左侧的噪声乘以$ \mathbf{H} $之后，取值范围不会过多的增长，仍然可以等于右侧的噪声取值范围。

GSW Key Equation的证明

接下来，我们和之前一样，尝试证明这一Key Equation的正确性。

首先，加法和之前是一样的，原本的$ \mathbf{H} $矩阵是由两个identity matrix构成，自然是small的： $$ [\mathbf{A}1 - x_1 \mathbf{G} \vert \mathbf{A}2 - x_2 \mathbf{G}] \cdot \underbrace{\begin{pmatrix}\mathbf{I}\ \mathbf{I} \end{pmatrix}}{\mathbf{H}{+, x_1, x_2}} = \underbrace{(\mathbf{A}1 + \mathbf{A}2)}{\mathbf{A}+} - (x_1 + x_2) \mathbf{G} $$ 唯一不同的是乘法，因为我们需要保证相乘的时候，$ \mathbf{A}_2 $是small的，所以我们需要额外的加入一次二进制分解，使得满足解密的正确性： $$ [\mathbf{A}_1 - x_1 \mathbf{G} \vert \mathbf{A}2 - x_2 \mathbf{G}] \cdot \underbrace{\begin{pmatrix}\mathbf{G}^{-1}(\mathbf{A}2)\ x_1\mathbf{I} \end{pmatrix}}{\mathbf{H}{\times, x_1, x_2}} = \underbrace{\mathbf{A}1 \mathbf{G}^{-1}(\mathbf{A}2)}{\mathbf{A}\times} - x_1x_2 \mathbf{G} $$ 此时，我们的$ \mathbf{H} $矩阵仍然是small的，符合Lemma II的要求。

实现了加法与乘法之后，我们就可以跟之前一样，扩展到同态计算任意的functionality $ f $了。

Q.E.D.

GSW Key Equation的含义

我们在这里再次列出GSW的Key Equation： $$ \forall \mathbf{A}i, \forall x, \forall f, \exists \text{ small } \mathbf{H}{f,x}:\ [\mathbf{A}_1 - x_1 \mathbf{G} \vert \cdots \vert \mathbf{A}n - x_n \mathbf{G}] \cdot \mathbf{H}{f,x} = \mathbf{A}_f - f(x) \mathbf{G} $$ 这一行等式直接概括了GSW中所做的同态计算的根本原理，并且给了我们一个非常好的视角来重新理解GSW的构造。

乍一看这个公式，似乎我们并不能用来直接做什么。其实这个Key Equation最重要的地方在于，它直接告诉我们，GSW拥有两种不同的计算functionality $ f $的方法！

假如我们拥有一系列的密文$ \mathbf{A}_i $，然后我们想要在密文上计算某个$ f $的话，第一种计算方法是最直观的，就是我们之前就了解的GSW的同态计算。我们只需要把要计算的$ f $拆分成一个个小的加法与乘法，然后再根据之前我们学习的方法来同态的计算它们，最后生成密文$ \mathbf{A}_f $。这种方法的好处在于，即使我们不知道密文中加密的内容，我们也可以直接通过结合密文来计算$ f $。

然而，第二种方法是这里的Key Equation额外告诉我们的：假如我们已经知道了这些密文加密的$ x_i $的值，那我们就可以通过推导出等式左侧的$ \mathbf{H}_{f,x} $矩阵来计算出相同的$ \mathbf{A}_f $出来！

这也就是说，我们可以通过两种方法来生成同一个密文的同态计算结果。其中一种方法只需要用到密文本身，而另一种方法则需要用到其中的原文。

GSW Key Equation的应用

在FHE系统中，我们之前即使不知道这个Key Equation的存在，仍然正常的学习了同态计算密文的方法。这是因为GSW Key Equation在FHE的应用场景中，我们只需要通过组合密文，计算出右侧的$ \mathbf{A}f $就足够了。等式左侧的$ \mathbf{H}{f,x} $的存在，只是为了整个FHE系统的correctness。之所以我们可以结合不同的密文同态计算某个functionality，正是因为这么一个$ \mathbf{H} $矩阵的存在。

我们上期讨论【BGG+14】的ABE结构时，我们也提到了类似的概念：我们通过计算$ \mathbf{A}_f $矩阵来签发密钥$ \mathbf{e}f $，随后使用类似于$ \mathbf{H}{f,x} $的线性变换在属性加密的密文上进行计算，得到一个类似于$ \mathbf{A}_f^t \mathbf{s} $的结果，最后使用密钥来解密。在【BGG+14】的ABE中，等式右侧的$ \mathbf{A}f $部分我们用于密钥生成（keygen），而左侧的$ \mathbf{H}{f,x} $部分我们则用于解密（decryption）。

最后，还有一个比较有趣的应用，即全同态签名（Fully Homomorphic Signatures，FHS），在【GVW15】中由Gorbonov，Vaikuntanathan与Wee提出。具体的应用方案和FHE差不多，我们假如签发了消息$ m $的签名$ \sigma $，那么我们就可以同态的计算某函数$ f $，得到一个$ f(m) $的签名$ \sigma_f $。在FHS中，等式右侧的$ \mathbf{A}f $部分用于签名的验证，而左侧的$ \mathbf{H}{f,x} $部分用于签署新的签名。

写在最后

$$ \forall \mathbf{A}i, \forall x, \forall f, \exists \text{ small } \mathbf{H}{f,x}:\ [\mathbf{A}_1 - x_1 \mathbf{G} \vert \cdots \vert \mathbf{A}n - x_n \mathbf{G}] \cdot \mathbf{H}{f,x} = \mathbf{A}_f - f(x) \mathbf{G} $$

这一期，学习的最重要的内容即GSW FHE的关键等式（Key Equation）。这个关键等式高度的概括了这个体系的精髓，从而让我们能够基于这个系统派生出各种各样的应用来。

下一期开始，我们就来看基于这个Key Equation而产生的第一个比较高级的应用：基于格的非交互零知识证明（NIZK）。