Lattice学习笔记07：SIS的效率与RingSIS

Ajtai OWF的参数大小

讨论完了Ajtai OWF（SIS）的安全性之后，现在问题来了：因为SIS问题的定义需要一系列的参数$ m, n, q $，如何定义这些参数，才可以满足之前的安全性证明呢？

Ajtai在96年的paper中指出来，只要$ m, n, q $足够大（large enough），那么$ f_\mathbf{A} $就是单向/collision resistant的。对于$ m, n $的值我们不去变它，因为这个决定了矩阵的维度。但是$ q $这个模组的大小，其实对于Ajtai OWF的安全性来说，差异是不会有太大的，所以大家的目光都放在如何尽可能的压缩$ q $的大小。在这篇paper中，Ajtai要求$ q = n^{O(1)} $，才可以满足安全性证明。

随后，在MR04这一篇paper中，Micciancio与Regev两个人进一步优化了这一证明，使得$ q \approx n^{2.5} $的情况下可以满足安全性。

在GPV08中，Gentry，Peikert，Vaikuntanathan三个大佬又对证明做了一次优化，使得$ q \approx n $的情况下仍然安全。

最后，在MP13中，Micciancio与Peikert把$ q $的大小压到了更小。在paper中，他们指出只要$ q \ge \sqrt{n} $，那么Ajtai OWF就是安全的。原文中的定理是这样的：如果我们可以破解$ \sqrt{n} < q < n $情况下的$ f_\mathbf{A} $，那么我们就可以把这个破解算法当作一个blackbox，然后逐步破解更大的$ q $的Ajtai OWF，即模组为$ q’ = q^c : c > 1 $。

压缩SIS中的模组$ q $

接下来，我们可以看一下，如何通过反证法来保证$ q > \sqrt{n} $的情况下，Ajtai OWF（即SIS）是安全的。

首先，为了让构造和证明变得简单，我们假设OWF $ f_\mathbf{A}(\mathbf{x}) $只接受二进制的短向量输入，即$ \mathbf{x} \in {0, 1}^m $。然后我们假设我们拥有一个很强大的算法，可以轻易破解在固定参数的$ n, m, q $下的SIS问题$ A’(\mathbb{Z}^{n \times m}q) $。这个时候，我们就可以用这个算法作为一个黑盒（blackbox），来构造出一个新的算法，来破解$ q^2 $模组下的SIS问题$ A(\mathbb{Z}^{n \times m^2}{q^2}) $。

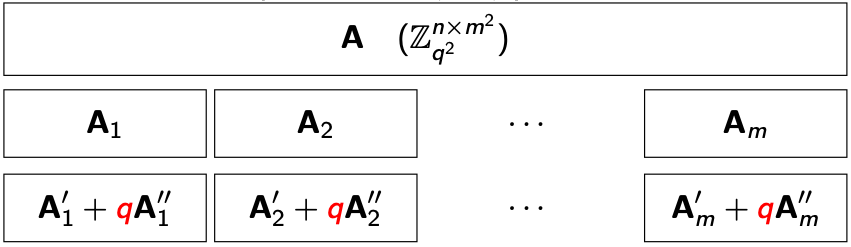
首先，我们拿到一个想要解决的SIS实例$ A(\mathbb{Z}^{n \times m^2}_{q^2}) $。然后我们把它平均的横向切割成$ m $份。

注意这个时候拿到的矩阵$ \mathbf{A}_1, \dots, \mathbf{A}_m $都是基于$ q^2 $的模组的，我们需要想办法把它转化为$ q $模组的。实现的方法其实不难，我们只需要把每一个$ q^2 $模组下的值$ c $拆分成$ c’ + q \cdot c’’ $就可以确保这些值都在$ q $的模组内了。具体来说，我们就可以把一个矩阵$ \mathbf{A}i \in \mathbb{Z}{q^2}^{n \times m} $拆分成$ \mathbf{A}_i’ + q\mathbf{A}_i’’ $。

这个时候，我们可以把$ m $个矩阵$ \mathbf{A}_i’ $放到我们之前的黑盒中，得到$ \mathbf{z}_i $并且满足： $$ \mathbf{A}_i’ \mathbf{z}_i = 0 \text{ mod }q\ \mathbf{z}_i \in {0, \pm1} $$ 这样一来，我们可以把得到的$ m $个解$ \mathbf{z}_i $和另外的矩阵$ \mathbf{A}_i’’ $结合起来，组成一个新的向量$ \mathbf{b}_i $： $$ \mathbf{b}_i = \frac{1}{q}(\mathbf{A}_i’ + q\mathbf{A}_i’’)\mathbf{z}_i = \mathbf{A}_i’’\mathbf{z}_i \in \mathbb{Z}_q^n $$ 我们把这些向量拼接在一起，组合成一个新的SIS问题矩阵$ \mathbf{B} $： $$ \mathbf{B} = [\mathbf{b}_1, \dots, \mathbf{b}_m] $$ 随后使用我们的黑盒，再次找到SIS问题的解$ \mathbf{w} $，即满足$ \mathbf{B} \mathbf{w} = 0 \text{ mod }q $。

当我们得到了$ \mathbf{z}i $和$ \mathbf{w} $之后，目标SIS问题的解就是这两个向量之间的tensor product，即： $$ (\mathbf{w} \otimes \mathbf{z}*) = (\mathbf{w}_1 \cdot \mathbf{z}_1, \dots, \mathbf{w}_m \cdot \mathbf{z}_m) \in {0, \pm1}^{m^2} $$ 具体的正确性证明在这里就不多说了。不过意会到这一证明的精髓之后，我们会发现其实$ q $的大小可以被压缩到很小很小，但是再往下的lower bound就需要更复杂的证明过程。

如果我们把$ q $压缩到最小，即二进制$ q = 2 $，那么这个情况下的LWE/SIS问题就被称作LPN问题（Learning Parity With Noise）。LPN问题也被认为是一个难题，但是现在似乎还没有很好的证明。

Ajtai OWF的运行效率

接下来我们可以看一看SIS系统的运行效率。

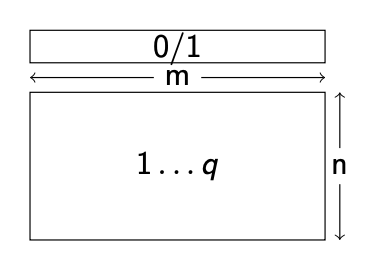
我们知道，验证一个SIS问题需要两部分：

1. 第一部分是SIS的问题矩阵$ \mathbf{A} $，大小由$ n, m, q $来决定。如果在Ajtai原版的假设中，$ q = n^{O(1)}, m = O(n \log{n}) > n \log_2{q} $。在这里，我们可以假设$ n = 64, q = 2^8, m = 1024 $。
2. 第二部分就是我们的OWF输入向量$ \mathbf{x} $，如果在二进制短向量的假设下，那么输入的就是$ m $个bits。

我们观察发现$ f_\mathbf{A} $实质上是一个把1024 bits的输入空间映射到512 bits的输出空间的一个压缩函数。（这里512由$ n \times \log_2(q) = 512 $计算而来。）

在OWF的使用场景中，矩阵$ \mathbf{A} $则是我们OWF的key，这也就是说我们的key的大小就是$ nm \log{q} = 2^6 \cdot 2^{10} \cdot 2^3 = 2^{19} = 64 \text{ KB} $。这对于一个小的OWF来说，key的大小有点太大了。同样，如果我们计算OWF的时候，矩阵相乘需要做$ nm = 2^{16} $次乘法，这也是非常巨大的一个数字。

这就是为什么Lattice的诟病一直是效率低的原因。因为我们使用了一个二维的矩阵，所以我们做任何矩阵相乘运算的时候，复杂度一直都是$ O(n^2) $的。

那么有没有什么方法可以让我们低于这个复杂度，并且压缩密钥的大小呢？

消减密钥矩阵大小

如果之前存储与计算的瓶颈一直都在矩阵的大小上面，那么有没有办法消减矩阵的大小呢？

有一个很好的idea就是，如果我们并不全部随机生成整个矩阵，而是随机生成一部分，另一部分用一定的伪随机生成或者线性变换来生成，就可以大大的缩小密钥的大小了（不需要存储整个矩阵）。同时，如果根据短密钥延伸出来的大矩阵拥有某些数学特性，说不定我们也不需要通过矩阵相乘的办法来计算SIS OWF的输出。

基于这个idea，可以构想出一个最简单的构造：我们就只需要随机生成$ \mathbf{A} $中的一行（甚至更短），然后把这一行作为一个PRG的种子，随机的生成整个OWF的密钥$ \mathbf{A} $。这样的话，我们的存储成本就变得很低，但是计算成本还是一样的，甚至会因为PRG的运算变得更差。这是因为PRG生成的数值都是近似随机的，没有任何数字之间的联系。所以我们对于一个随机生成的矩阵进行运算的话，只能通过矩阵相乘，即$ O(n^2) $的方法来完成。

第二个比较有意思的idea，就是我们可以随机生成一个向量$ \mathbf{a}^{(i)} $，然后通过不停的旋转这一行向量的值，逐渐构成一个小的循环密钥矩阵$ \mathbf{A}^{(i)} $： $$ \mathbf{a}^{(i)} = [\mathbf{a}_1^{(i)}, \mathbf{a}_2^{(i)}, \dots, \mathbf{a}_n^{(i)}]\ \mathbf{A}^{(i)} = \begin{bmatrix} \mathbf{a}_1^{(i)} & \mathbf{a}_n^{(i)} & \cdots & \mathbf{a}_2^{(i)}\ \mathbf{a}_2^{(i)} & \mathbf{a}_1^{(i)} & \cdots & \mathbf{a}_3^{(i)}\ \vdots & \vdots & \ddots & \vdots\ \mathbf{a}n^{(i)} & \mathbf{a}{n-1}^{(i)} & \cdots & \mathbf{a}1^{(i)}\ \end{bmatrix} $$ 当我们生成这么一个循环密钥矩阵之后，我们如法炮制，一共生成$ m/n $个矩阵，然后把它们横向拼接在一起，形成我们的密钥矩阵$ \mathbf{A} $： $$ \mathbf{A} = [\mathbf{A}^{(1)} \vert \mathbf{A}^{(2)} \vert \dots \vert \mathbf{A}^{(m/n)}] $$ 这个系统在M02（Micciancio）中被第一次提出，并且指出如果$ n, m, q $的维度选择合适的话，这样体系下的$ f\mathbf{A} $是单向的。这一系统的构造也和1998年提出的很有名的NTRU加密系统很相似。

我们构造出的矩阵$ \mathbf{A} $就是一堆小的循环矩阵拼接而成的，虽然这种形式下面构造的OWF的单向性可以被轻易证明，但是比较难的另一个安全属性是collision resistance。为了证明这一点，这个idea的核心思路就是：我们通过改变循环矩阵的生成方法，进而确保$ \Lambda_q^\perp(\mathbf{A}) $中的SVP问题很难解决，然后证明$ f_\mathbf{A} $是collision resistant的。

循环矩阵的Collision Resistance

首先，我们来看一看我们刚刚提出来的循环矩阵的构造，能否满足CR这一要求。

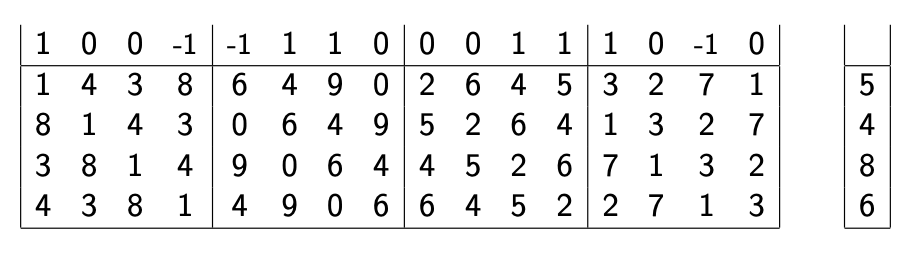
举个例子，假设我们有上图这么一个循环矩阵结构下的SIS OWF的矩阵$ \mathbf{A} \in \mathbb{Z}_q^{4 \times 16} $，并且给定了一组OWF的输入$ \mathbf{x} \in \mathbb{Z}q^{16} $。我们能否找到这个输入的另一组collision，即找到另一个$ \mathbf{x}’ \in \mathbb{Z}q^{16} \ne \mathbf{x} $，使得$ f\mathbf{A}(\mathbf{x}’) = f\mathbf{A}(\mathbf{x}) $呢？

乍一看，这么大一个矩阵，似乎没有什么头绪。如果我们直接去找这个矩阵的inverse，那么也要花费很长的时间。正确的方法是利用SIS OWF的线性组合特性，即$ f_\mathbf{A}(\mathbf{x} + \mathbf{y}) = f_\mathbf{A}(\mathbf{x}) + f_\mathbf{A}(\mathbf{y}) $。

如果我们要找到另一个collision的话，我们只需要求解这个矩阵$ \mathbf{A} $的SIS问题的结果，即找到一个二进制短向量$ \mathbf{y} $，使得$ \mathbf{Ay} = 0 \text{ mod }q $。然后我们就可以轻松的通过组合这个SIS的解和原本的输入的方式，得到另一个collision：$ \mathbf{x’ = x + y} $。这里为了保证二进制短向量的特性，我们相加两个向量之后需要做一些求模的处理。

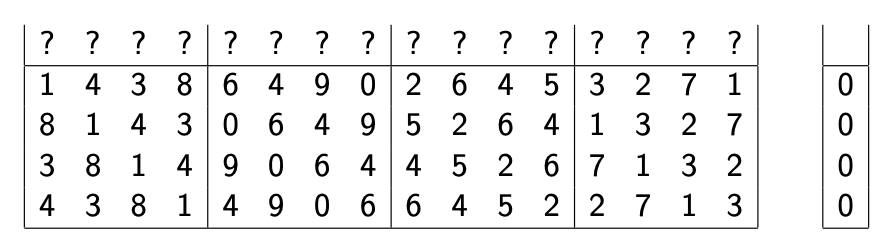
找到这一条路之后，接下来的问题就是求解SIS问题了，即找到一个二进制短向量$ \mathbf{y} $使得$ \mathbf{Ay} = 0 \text{ mod }q $。我们可以观察一下，这4个小的旋转矩阵分别都是由四个独立的向量$ [1,4,3,8], [6,4,9,0], [2,6,4,5], [3,2,7,1] $组成的。因为这些旋转操作都是有规律的，我们会发现其实循环矩阵中每一列的值加起来都是相同的。这也就是说，如果我们让$ \mathbf{A} $乘以一个全是1的向量，我们就会得到四组参数相等的向量：

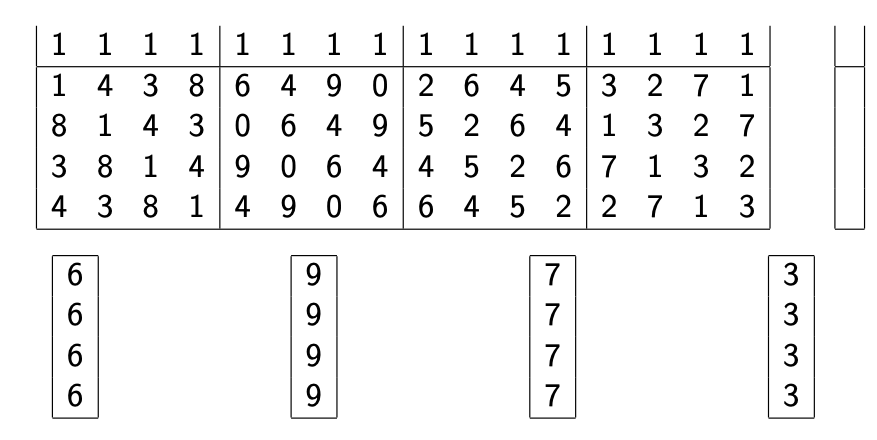
我们观察发现，如果我们全部乘以1的话，就可以得到$ 6, 9, 7, 3 $这四个数字。现在的问题就变成了，我们能否找到一组$ {0, \pm1} $以内的参数赋值，使得这些参数乘以这四个数字加起来最后可以等于0呢？这有点像是一个算24点问题了。很简单我们就可以找到： $$ 1 \times 6 -1 \times 9 + 0 \times 7 + 1 \times 3 = 0 $$ 这也就是说，我们SIS问题的解就是： $$ \mathbf{y} = \begin{bmatrix} 1&1&1&1&-1&-1&-1&-1&0&0&0&0&1&1&1&1 \end{bmatrix} $$ 得到这个解向量之后，我们就可以在原本的输入$ \mathbf{x} $的基础上加上或者减去这个解向量，就可以非常简单的计算出任意多种collision啦。

循环矩阵到多项式

为什么上面构造的循环矩阵的SIS问题这么简单呢？这是因为我们可以对这个矩阵做进一步的分解，即观察到他们每一列加起来的值都相等这一特性，把问题简化。

为什么可以做这个简化呢？我们首先观察一下最左侧的循环矩阵： $$ \widetilde{\mathbf{R}} =\begin{bmatrix} 1&4&3&8\ 8&1&4&3\ 3&8&1&4\ 4&3&8&1 \end{bmatrix} $$ 我们的初始生成向量为$ [1,8,3,4] $，这也就是说，这个向量的第一个元素1被分配在了矩阵的正对角线上，然后后面的元素依次分配在对角线周围。我们其实可以用一个旋转矩阵$ \mathbf{X} $来表述这一变换的过程： $$ \mathbf{X} = \begin{bmatrix} 0&0&0&1\ 1&0&0&0\ 0&1&0&0\ 0&0&1&0 \end{bmatrix} $$ 如果我们反复叠加这一旋转矩阵，就可以从1的位置旋转到8的位置，然后再旋转到3的位置，等等。这样一来，我们可以用一组线性组合来表示$ \widetilde{\mathbf{R}} $： $$ \widetilde{\mathbf{R}} = 1 \cdot \mathbf{I} + 8 \cdot \mathbf{X} + 3 \cdot \mathbf{X}^2 + 4 \cdot \mathbf{X}^3 $$ 这其实就是基于旋转矩阵$ \mathbf{X} $的一组$ n-1 $阶的多项式！如果我们使用更加通用的表达方式的话，那就是： $$ \widetilde{\mathbf{R}} = a_1 I_n + a_2X + \dots + a_nX^{n-1} $$ 循环矩阵$ \widetilde{\mathbf{R}} $可以被表述成$ n-1 $阶多项式的形式，并且这一结构与$ \mathbb{Z}[x]/(x^n-1) $的多项式环是同构（isomorphic）的。这也就是说，我们可以使用一组最多为$ n-1 $阶，每一项系数在$ q $以内的多项式来代替我们的循环矩阵$ \widetilde{\mathbf{R}} $。

我们还注意到，当旋转的次数变得过多（超出了$ n-1 $阶）之后，旋转到最下侧的数字会回到最上面来。这一点我们可以在这个多项式环中的乘法上定义： $$ x \cdot x^i = \begin{cases} x^{i+1} & i < n-1\ 1 & i = n-1 \end{cases} $$ 因为我们在$ x^n -1 $的环中，$ x^n $比我们的环的大小$ x^n-1 $要大1，所以说$ x^n = 1 \text{ mod } (x^n - 1) $。

当我们把$ \widetilde{\mathbf{R}} $用多项式表达之后，我们就会发现，$ x^n - 1 $这一多项式，其实是很好约分的： $$ x^n - 1 = (x-1) \cdot (x^{n-1} + \dots + 1) $$ 这就是为什么我们可以非常简单的找到SIS的解，因为我们可以很简单的找到这个多项式环中的0交界点。

多项式到RingSIS

因为我们发现循环矩阵$ \widetilde{\mathbf{R}} $可以很好的被多项式环代替，我们索性就把原本的SIS OWF的key矩阵变成$ k = m / n $个多项式拼接在一起。同理，我们把OWF的输入矩阵也变成$ k $个多项式： $$ f_{\mathbf{a}_1, \dots, \mathbf{a}_k}(\mathbf{u}_1, \dots, \mathbf{u}_k) = \sum_i \mathbf{a}_i(X) \cdot \mathbf{u}_i(X) \text{ mod } (X^n - 1)\ \mathbf{a}_i, \mathbf{u}_i \in R = \mathbb{Z}[X]/(X^n - 1) $$ 这样以来，我们就可以通过多项式相乘的方法来计算原本的循环矩阵版的SIS OWF了。随后得到的值也会是一样的，因为我们可以代入原本的旋转矩阵$ \mathbf{X} $为这里多项式中的取值$ X $，然后等式全部成立。

我们把这样的，通过多项式环中相乘（而不是矩阵相乘）的类似SIS问题，称之为RingSIS。

RingSIS的好处是什么呢？首先，这和之前的循环矩阵的优势一样，我们只需要存储一组随机的向量（即多项式的参数赋值），就可以定义整个问题，这样的存储成本就很低。

其次，多项式环中还有一个之前矩阵形式里不能实现的黑科技：多项式之间相乘可以通过FFT（快速傅立叶变换）来达到$ \tilde{O}(n) $的效率。比起矩阵相乘$ O(n^2) $的效率来说，是质一般的飞跃。

现在基于格的很多库都是基于多项式环来进行运算的，因为运算效率高，存储成本低。

更安全的多项式环

在RingSIS中，我们可以任意选择想要的多项式环。因为我们之前发现了$ X^n - 1 $这个环很好约分，所以对应的OWF容易被找到collision，所以我们可以考虑，换一个更加安全的环。

为了通俗的表达各种多项式环，我们一般都把RingSIS问题中的环用$ \mathbb{Z}[X]/p(X) $来表示，其中$ p(X) $就是任意一个monic polynomial。

如果$ p(X) $不能被进一步约分，那么我们就不能用同样的方法来更快速的找到collision。这样的话我们就可以把不能约分的多项式环下的RingSIS问题的难度规约到理想格（ideal lattice）中的SVP问题上来了。

一个比较简单的例子就是$ \mathbb{Z}[X]/(X^n + 1) $。这个环和之前的环一样，也包括了所有的$ n-1 $阶的多项式。唯一不一样的，是乘法的定义： $$ x \cdot x^i = \begin{cases} x^{i+1} & i < n-1\ -1 & i = n-1 \end{cases} $$ 在得到临界值$ x^n $的时候，因为我们的环的大小就是$ x^n + 1 $，比$ x^n $大1，所以我们可以用-1来表示。这样一来，和之前一样是一个Ring的结构，只是乘法的定义有所改变。

在这种方式下，对应的循环矩阵$ \widetilde{\mathbf{R}} $就是： $$ \widetilde{\mathbf{R}} =\begin{bmatrix} 1&-4&-3&-8\ 8&1&-4&-3\ 3&8&1&-4\ 4&3&8&1 \end{bmatrix} $$ 根据多项式的特性，只要$ n = 2^k $，即2的幂，$ X^n + 1 $这一多项式是不能被约分成更小的式子的。所以这种构造下的RingSIS，或者循环矩阵拼接成的SIS OWF，就是单向并且Collision Resistant的啦。

Credits

The contents of this post is summarized from Prof. Daniele Micciancio’s lecture at Simon’s Institute Lattice Bootcamp.