Lattice学习笔记03：对偶格（Dual Lattice）

对偶格（Dual Lattice）

线性空间里面一个很重要的概念就是对偶空间（Dual Space）。一个线性空间$ V \in \mathbb{R} $的对偶空间就包括了所有从$ V \rightarrow \mathbb{R} $的线性变换函数。

同理可得，一个Lattice也有它对应的对偶空间，即这个空间中的每一个元素都是一个把这个格中的元素$ \mathbf{v} \in \mathcal{L} \rightarrow \mathbb{Z} $映射到整数空间中的线性变换。一般来说我们可以用一个向量来表达线性变换，所以也就是说一个Lattice的对偶空间就是一组向量，而这些向量乘以格中的任意格点，都可以得到一个$ \mathbb{Z} $中的元素。

再换句话来说，也就是说这些对偶的向量，乘以任意Lattice中的格点向量，都能得到一个整数。这些向量本身就组成了另一个Lattice，我们把这个新的Lattice成为对偶格（Dual Lattice）。

系统性的定义的话，一个Lattice $ \Lambda $的对偶格$ \Lambda^\vee $就是一组向量$ \mathbf{x} \in span(\Lambda) $并且满足： $$ \forall \mathbf{v} \in \Lambda: \langle \mathbf{x}, \mathbf{v} \rangle \in \mathbb{Z} $$ 我们拿最常见的笛卡尔整数格$ \mathbb{Z}^n $举个例子。

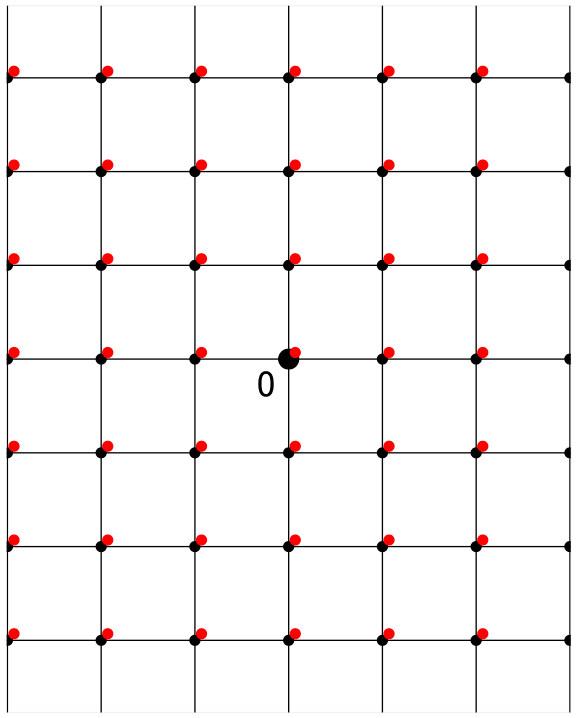
由于$ \mathbb{Z}^n $中的每个格点对应的向量都是整数，所以任何整数向量和它的乘积也都是整数，即： $$ (\mathbb{Z}^n)^\vee = \mathbb{Z}^n $$ 我们在上面的图中可以看出，这个格与它的对偶格是一样的，所以格点都重合了。

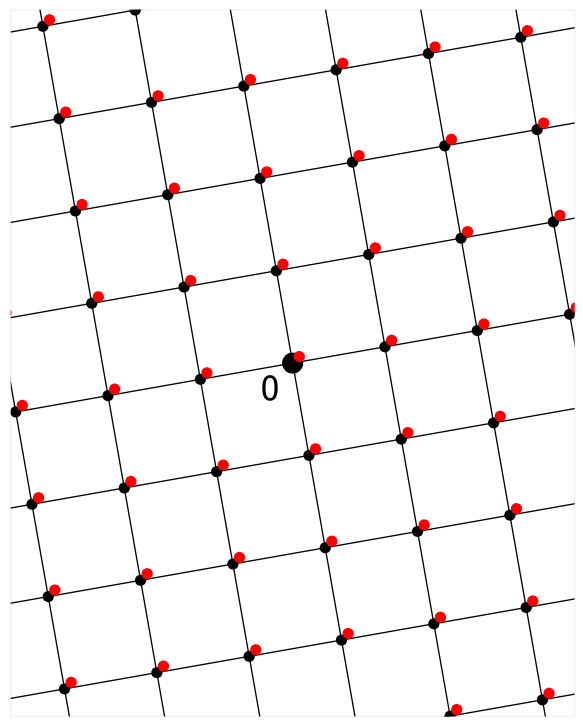
如果我们给原来的格叠加了一个线性变换$ \mathbf{R} $（这里是旋转），那么新的Lattice $ \mathbf{R}\Lambda $的对偶格可以通过旋转变换原本的对偶格来得到。 $$ (\mathbf{R}\Lambda)^\vee = \mathbf{R}(\Lambda^\vee) $$ 这个原因也很简单，假如我们拥有在$ \Lambda $中的格点与对偶格点$ \mathbf{v, x} $，和一组在$ \mathbf{R}\Lambda $中的$ \mathbf{v’, x’} $。已知了$ \mathbf{v’} $是旋转了$ \mathbf{v} $得到的。因为旋转一对向量并不会改变向量之间的乘积，所以我们只需要对应的旋转$ \mathbf{x} $，即$ \mathbf{Rx} $，就能保证乘积不变，也能得到整数。 $$ \mathbf{v’} = \mathbf{Rv}\ \mathbf{x’} = \mathbf{Rx}\ \langle \mathbf{v, x} \rangle = \langle \mathbf{v’, x’} \rangle $$ 同理可得，如果我们缩放了一个Lattice $ \Lambda $，使得它的格点扩大/缩小了$ q $倍的话，为了保证点乘的乘积相同，最后得到的对偶格的大小就要对应的变成$ q/1 $倍。 $$ (q \cdot \Lambda)^\vee = \frac{1}{q} \cdot \Lambda^\vee $$ 仔细观察可以发现，不管是什么样的Lattice，格和对偶格之间有一些基本的关系： $$ \Lambda_1 \subseteq \Lambda \iff \Lambda_1^\vee \supseteq \Lambda_2^\vee\ (\Lambda^\vee)^\vee = \Lambda $$ 我们可以把对偶格理解成是一个格的“倒数”，因为很多时候它们之间的关系是反过来的。

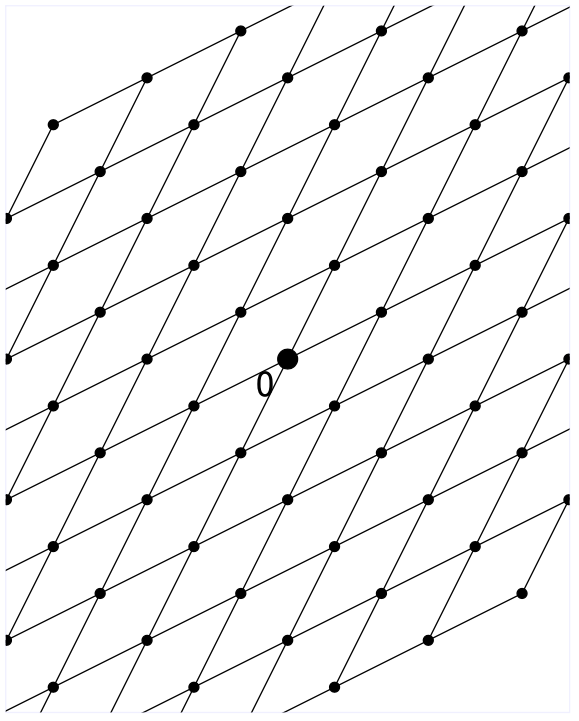
在笛卡尔整数格$ \mathbb{Z}^n $中，对偶格看起来很好理解，因为和原本的格长得也差不多。但是实际上对偶格和格本身其实并没有太大的几何上的关联，我们最好把对偶格里面的每一个向量理解成一个“线性变换函数“，而不是一个几何上的格点。

比如说上图中这个斜过来的格，它的对偶格就和本身没有任何几何上的关联。

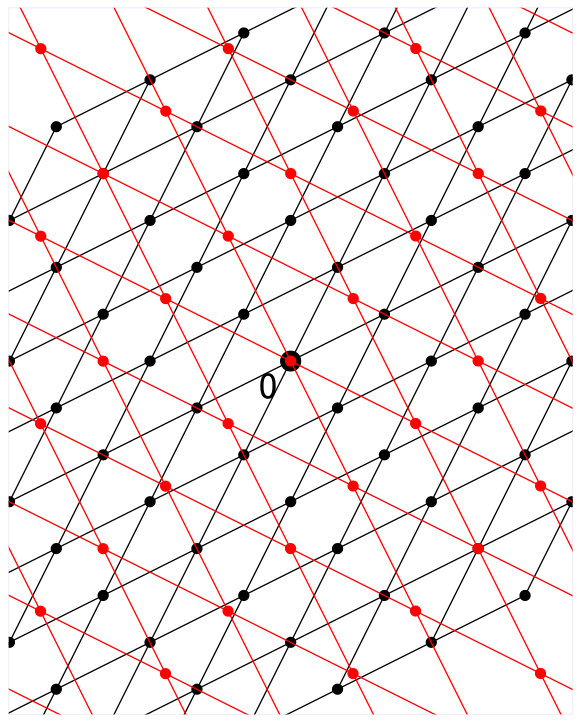
我们只需要牢记格与对偶格之间唯一需要满足的就是任意两个格点之间相乘，乘积一定是在$ \mathbb{Z} $中的整数。并且只有相乘这个操作有意义，加法是没有几何意义的。

Lattice分层

当我们得到了一个Lattice $ \Lambda $的对偶格$ \Lambda^\vee $之后，我们可以做一件很有趣的事情：给原有的Lattice分层。

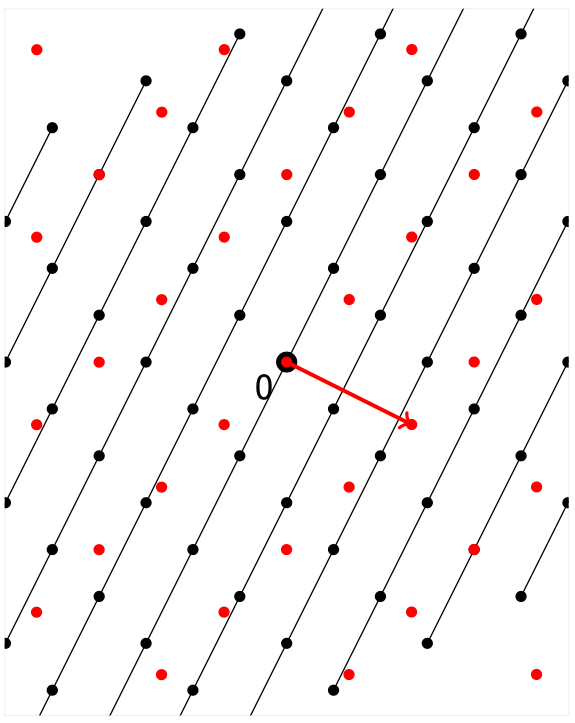
我们知道对偶格中的每一个格点都可以和原本的格中的任何格点相乘并且得到一个整数。我们可以选定一个对偶格中的点$ \mathbf{v} \in \Lambda^\vee $，然后让原本的格中的所有点都和这个点相乘。最后我们观察所有的乘积结果的大小，并且把所有得到相同结果的格点都分为“一层”$ L_i $。 $$ L_i = \left{\mathbf{x} \in \Lambda: \mathbf{x} \cdot \mathbf{v} = i\right} $$ 接着，如果我们再选取另一个对偶格中的点$ \mathbf{v’} $，然后又可以得到另一组不一样的分层。

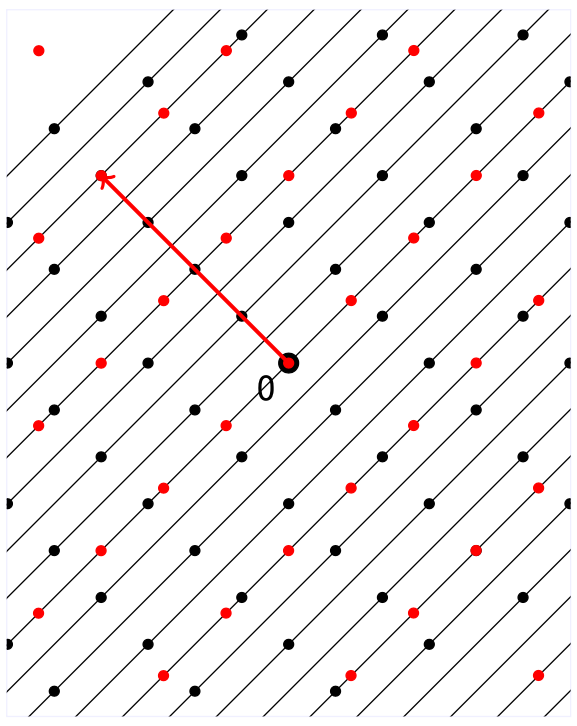
我们观察会发现，这个分层的密度和层与层之间的距离都不一样。这个距离，其实是与选取的对偶格中的向量$ \mathbf{v} $的长度成反比的。 $$ Dist(L_i, L_{i+1}) = \frac{1}{\lvert \lvert \mathbf{v} \rvert \rvert} $$ 这代表了什么呢？我们可以用对偶格向量的长度来逼近原本的$ \Lambda $这个格的覆盖半径！

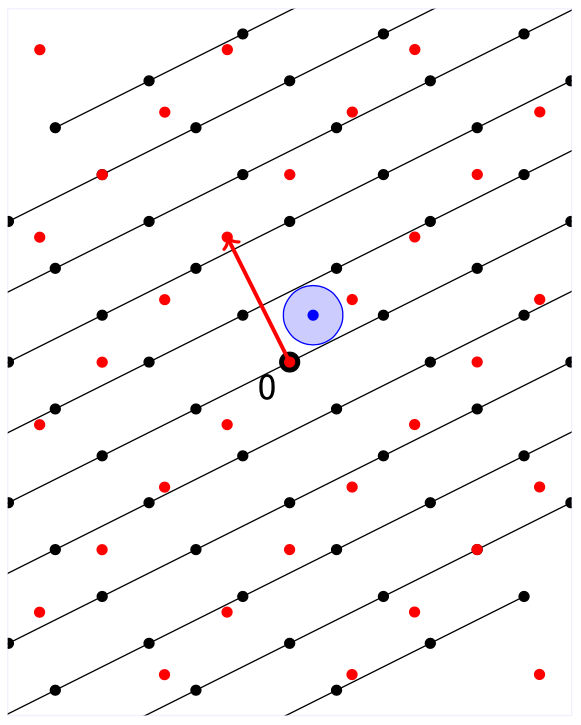$$ \mu(\Lambda) \ge \frac{1}{2 \lvert \lvert \mathbf{v} \rvert \rvert} $$ 我们知道，所有的$ \Lambda $中的格点都只能在每一层上面，所以层与层之间的缝隙里是不会有任何格点的。同理我们就可以塞一个圆进去，而这个圆的半径一定得小于等于整个格的覆盖半径。

这是因为，覆盖半径是在$ \mathbb{R}^n $空间中任意选取一个点，这个点到附近的格点的最远距离。因为我们知道了对偶格点构成的分层之间的距离，所以覆盖半径肯定要大于等于这个距离。

这也就是说，我们可以在这个对偶格中任意选择一个点，然后找到对应的分层距离，就可以逼近原本的格的最大半径了。因为选择的$ \mathbf{v} $的长度越短，我们得到的分层距离越大，所以理论上这个对偶格$ \Lambda^\vee $的最短向量$ \lambda_1(\Lambda^\vee) $构成的分层距离，就是我们能逼近的最大上限了。这也就是说，如果$ \lambda_1(\Lambda^\vee) $比较短的话，那么$ \mu(\Lambda) $对应的也会比较大。反之也是如此。

Banaszczyk定理

我们之前观察到的Lattice的覆盖半径的大小与对偶格的最短向量长度的反比例关系，被Banaszczyk总结成了定理。首先，对于任何的Lattice $ \mathcal{L} $： $$ 1 \le 2 \lambda_1(\mathcal{L}) \cdot \mu(\mathcal{L}^\vee) \le n $$ 这一点规定了覆盖半径与对偶格最短向量这两个值之间的乘积一定会在一个$ n $上限的范围内。同时，我们不仅可以对应最短的向量与最大的覆盖半径，我们还可以对应其他的短向量： $$ 1 \le \lambda_i(\mathcal{L}) \cdot \lambda_{n-i+1}(\mathcal{L}^\vee) \le n $$ 这也就是说，我们可以把一个格中的最短向量和它的对偶格中的最短向量一一对应起来，找到它们之间的关系。如果我们要找一个格$ \Lambda $的最短向量$ \lambda_1 $，我们不妨先找到对偶格$ \Lambda^\vee $的覆盖半径$ \mu(\Lambda^\vee) $，然后再根据上面的关系式来逼近我们想要的结果。

BDD问题规约到SIVP

学习完对偶格（Dual Lattice）的概念之后，我们就可以把上一篇笔记中看过的BDD问题，即至多只有一个解，并且搜索的半径小于$ \lambda_1/2 $的CVP问题，规约到SIVP问题上来。

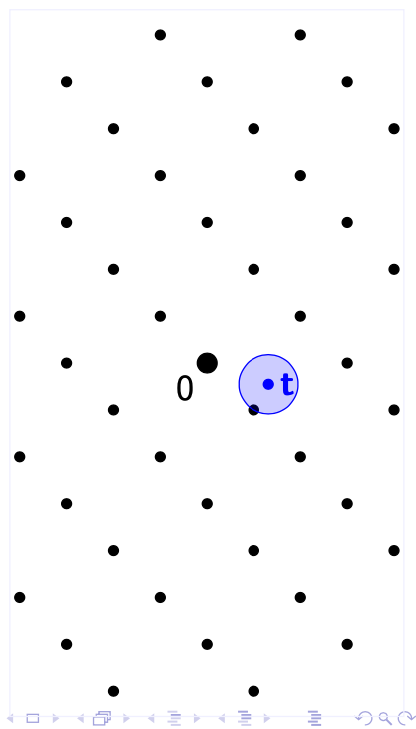
首先，假设我们在一个格$ \Lambda $中，给定一个$ \mathbb{R}^n $中的随机点$ \mathbf{t} $，然后求解BDD。

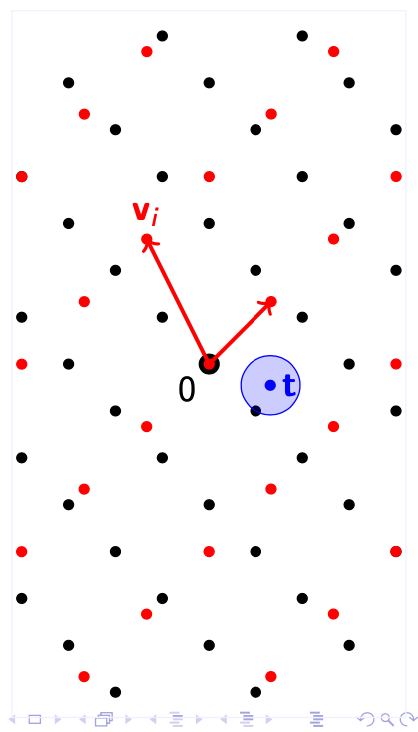
我们第一步可以做的是，先找到这个格的对偶格$ \Lambda^\vee $，并且在这个对偶格中求解SIVP问题，得到对应的一组最短向量$ \mathbf{V} = SIVP(\Lambda^\vee) $。

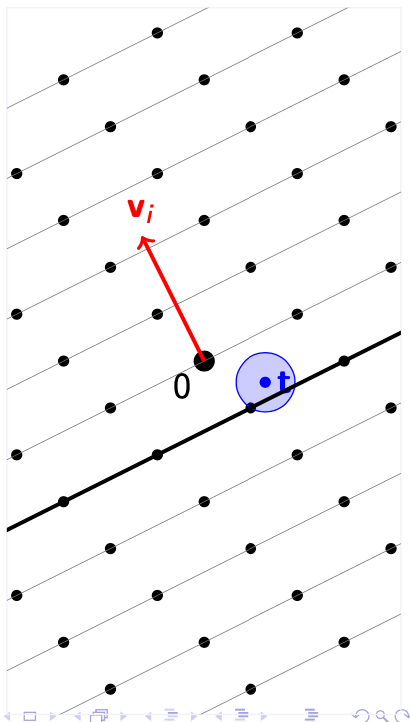
得到这一组最短向量$ \mathbf{V} $之后，我们依次选择其中的每一个向量$ \mathbf{v}_i $，然后根据这个向量对于格$ \Lambda $进行分层，然后找到距离$ \mathbf{t} $最近的一层$ L_i $。上图展示了第一个向量得到的分层。

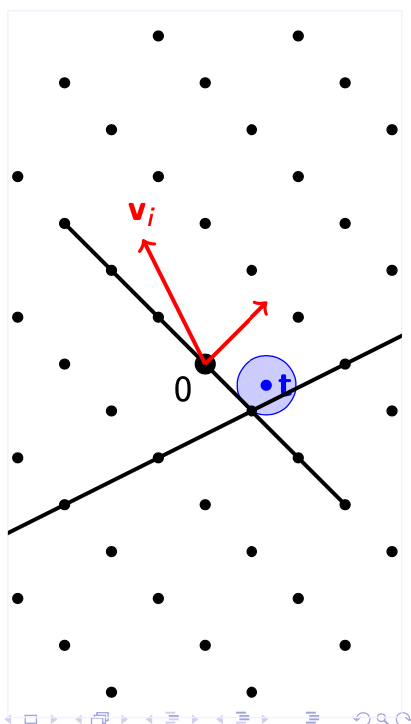
当我们重复这个操作$ n $次之后，就会得到$ n $个不同的分层。这个时候我们就可以把这些分层的交汇点拿到，这就是BDD问题的解了。这是因为SIVP的解拿给我们的都是线性独立的向量，所以我们根据这个向量构成的$ n-1 $维的hyperplane分层之间也是相互独立的，这些平面也会相聚在一个点上。 $$ BDD(\Lambda, \mathbf{t}) = L_1 \cap L_2 \cap \dots \cap L_n $$ 这个依靠SIVP的算法基本上可以解决大部分BDD问题。但是为了确保我们输出的结果是BDD问题的正确解，我们还需要额外的加上一个约束： $$ \mu(\mathbf{t}, \Lambda) \le \frac{\lambda_1}{2n} \le \frac{1}{2\lambda_n^\vee} \le \frac{1}{2\lvert \lvert \mathbf{v}_i \rvert \rvert} $$ 我们需要规定这个BDD问题给定的向量$ \mathbf{t} $需要距离最近的格点在$ \frac{\lambda_1}{2n} $的范围之内的时候，这个方法就可以找到正确的解。这个不等式的后半部分可以根据上面的Banaszczyk定理得到。

这一约束，对于BDD问题原本的定义$ \mu(\mathbf{t}, \Lambda) \le \lambda_1/2 $要限制多了不少，但是已经是一个很强大的算法了。

Lattice中的模（Modulo a Lattice）

另一个对于对偶格的用处，在于Lattice的模运算。

我们知道一个Lattice $ \mathcal{L} $是一组在$ \mathbb{R}^n $中离散的格点。这些格点之间可以相加，并且最后还是会得到$ \mathcal{L} $中的格点。因为拥有这一特性，$ (\mathcal{L}, +) $被称为$ (\mathbb{R}^n, +) $的一个Additive Subgroup（加法子群？）。

因为这一特性，根据群理论，我们可以构成一个Quotient Group（商群？），即$ \mathbb{R}^n/\mathcal{L} $。

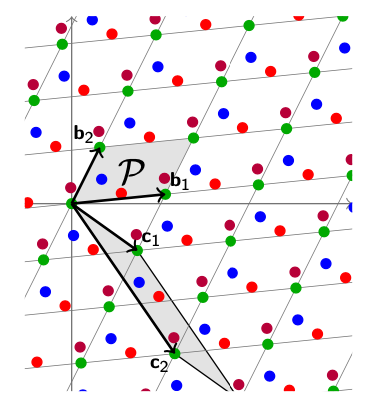
这个概念看起来比较烧脑，其实理解起来很简单。就像我们平时$ mod\ n $一样，我们可以把整个多维空间用这个Lattice的Determinant组成的多面体平分成多份。如果我们仔细观察上面图中$ \mathcal{P} $的阴影部分上覆盖的格点，会发现这上面的格点的分布规则和隔壁每一个一样的多面体上面的分布是一模一样的。

这也就是说我们可以把任何一个空间中的点使用格求模的方法，压缩到$ \mathcal{P} $这么大的范围中，并且这就足够表示这个点在空间中距离其他的格点的位置了。

同理可得，如果我们观察上图下方$ \mathbf{c_1, c_2} $组成的基形成的阴影部分，即Determinant组成的空间，我们会发现这一部分也可以很好的切割整个$ \mathbb{R}^n $的空间，所以我们也可以基于这一组基进行求模。

在这个Quotient Group中的一个向量，我们可以用$ \mathbf{t} + \mathcal{L} $来表示。

对于这个向量，我们其实还有另外一种表达方式： $$ (\mathbf{B}^\vee)\mathbf{t} \text{ (mod 1)} $$ 这个向量可以用对偶格的基向量乘上$ \mathbf{t} $得到的一个数字，然后取小数点部分来表示。注意这里因为$ \mathbf{t} $并不在格点上，所以对偶空间基向量乘上它不会得到整数。这个小数点后面的部分，就可以独立的代表这个Quotient Group中的每一个元素。这算是一个把群元素映射到$ \mathbb{R} $上的一种小技巧。

Credits

The contents of this post is summarized from Prof. Daniele Micciancio’s lecture at Simon’s Institute Lattice Bootcamp.