Lattice学习笔记02：格中难题

SVP问题（Shortest Vector Problem）

一个Lattice中最常见的问题，就是最短向量问题（SVP，Shortest Vector Problem）。问题的定义是这样的：给定一个基为$ \mathbf{B} $的Lattice $ \mathcal{L}(\mathbf{B}) $，找到一个这个基构成的格点$ \mathbf{Bx}: \mathbf{x} $，使得这个点距离0坐标点的距离最近。 $$ \mathbf{Bx}: \mathbf{x} \in \mathbb{Z}^k\ \lvert \lvert \mathbf{Bx} \rvert \rvert \le \lambda_1$$ 观察发现，因为$ \lambda_1 $已经是这个格中点和点之间的最短距离了，所以$ \mathbf{Bx} $距离0点的距离其实也不会小于$ \lambda_1 $，最多是等于罢了。

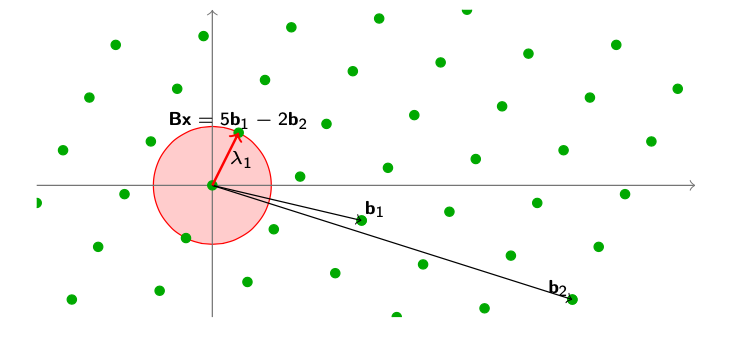
图中给出了一个比较经典的例子，加入我们拥有一组格的基向量$ \mathbf{B} = [\mathbf{b}_1, \mathbf{b}_2] $，我们可以找到一个点$ \mathbf{Bx} $，即$ 5\mathbf{b}_1 - 2\mathbf{b}_2 $对应的这个点，正好就是这个格的最短向量$ \lambda_1 $。

当然，如果我们拿到的基不是很好，其实计算严格的SVP（即找出$ \lambda_1 $）是一个很难的事情，所以SVP这个问题也有个宽松的版本：$ SVP_\gamma $。

在$ SVP_\gamma $中，问题的设定大致一样，但是唯一不一样的在于，我们找到的点$ \mathbf{Bx} $，并不一定需要恰好是最短向量$ \lambda_1 $，而只要满足小于等于$ \lambda_1 $的一个倍数$ \gamma $就行了。 $$ \mathbf{Bx}: \mathbf{x} \in \mathbb{Z}^k\ \lvert \lvert \mathbf{Bx} \rvert \rvert \le \gamma \lambda_1$$

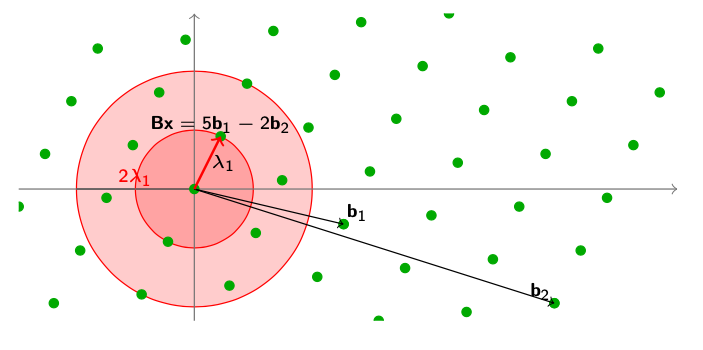
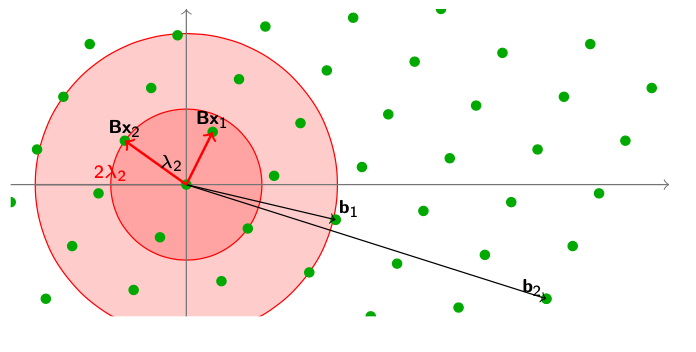
图上显示的就是当$ \gamma = 2 $的情况。这个时候我们的$ SVP_\gamma $问题就有很多个解了。

CVP问题（Closest Vector Problem）

Lattice中另一大常见的问题，就是最近向量问题（CVP，Closest Vector Problem）了。问题的定义是这样的：给定连续空间中任意的一个点$ \mathbf{t} $，找到距离这个点最近的格点$ \mathbf{Bx} $。

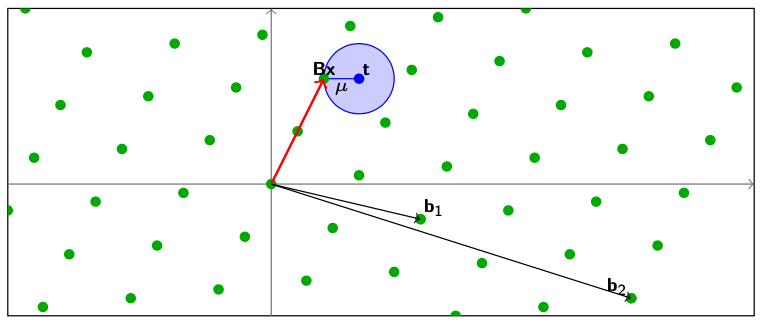$$ \mathbf{Bx}: \mathbf{x} \in \mathbb{Z}^k\ \lvert \lvert \mathbf{Bx - t} \rvert \rvert \le \mu$$ 这里我们的约束距离$ \mu $就是这个Lattice的覆盖半径（即所有可能的$ \mathbf{t} $中距离格点最长的距离）。同理可得，我们也可以得到CVP的宽松版，即$ CVP_\gamma $。

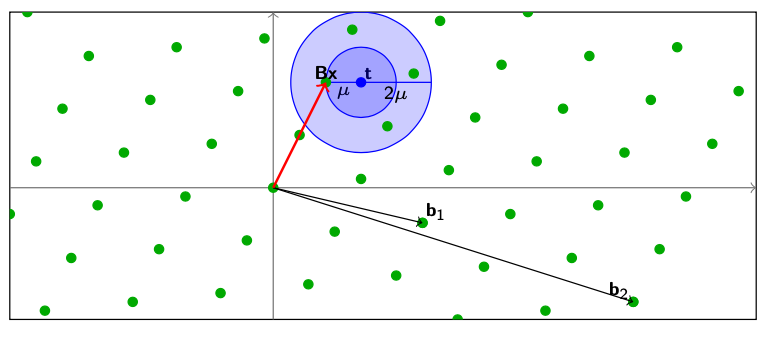$$ \mathbf{Bx}: \mathbf{x} \in \mathbb{Z}^k\ \lvert \lvert \mathbf{Bx - t} \rvert \rvert \le \gamma\mu$$ 加上一个宽松的参数$ \gamma $之后，CVP问题就会变得简单一些，解的数量也变多了。

SIVP问题（Shortest Independent Vectors Problem）

Lattice中第三大重要的问题，就是最短独立向量问题。问题定义：给定一个Lattice $ \mathcal{L}(\mathbf{B}) $，找到$ n $个线性独立的向量$ \mathbf{Bx_1, \dots, Bx_n} $并且这些向量的长度都要小于等于最长的最短向量$ \lambda_n $。 $$ \max_i \lvert \lvert \mathbf{Bx_i} \rvert \rvert \le \lambda_n$$

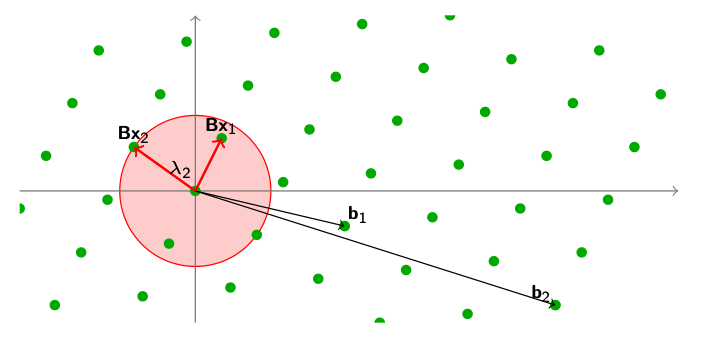
这个图就很好的表达了在$ n=2 $的情况下，我们找到了两个小于等于$ \lambda_2 $的点。和SVP与CVP问题一样，我们也可以给出SIVP问题的宽松版定义，即$ SIVP_\gamma $。在宽松版本中，我们只需要找到$ \gamma \lambda_n $范围内的就可以了。

基于Lattice的信息传输

学会了SVP，CVP，SIVP这三件套之后，就可以来了解一下如何通过Lattice来进行可靠的消息传输了。

我们要解决的问题是在一个有噪音的信道中可靠的传输信息（Reliable transmission of information over noisy channels）。结合Lattice的概念之后，其实实现起来很简单。

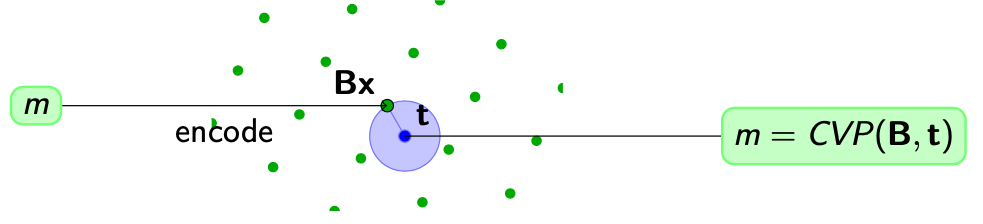
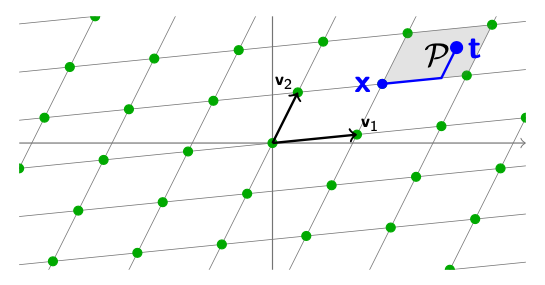
首先，我们把需要传输的消息映射到Lattice中的一个点上，即$ \mathbf{Bx} $，然后我们把$ \mathcal{L}, \mathbf{Bx} $发送出去。在接收端我们得到的数据会产生一定程度的偏移，在图上反馈出来就是偏移到了$ \mathbf{t} $这个点上。我们只需要解决CVP问题，就可以找到原本的格点$ \mathbf{Bx} $，然后就可以还原出$ m $了。

在解决CVP问题的时候，我们还需要知道这个Lattice中最短向量$ \lambda_1 $的值来判断CVP问题是不是能够求解出原本的那个点$ \mathbf{Bx} $。我们需要通过求解SVP问题来得到$ \lambda_1 $。

最后，SIVP问题在这里也有所适用。如果我们在传输的过程中为了压缩数据使用了向量量化（Vector Quantization）的方法，在重建向量的时候，需要用到SIVP的解来修复误差。

CVP问题的两种版本

我们再次系统性的定义一下CVP问题。

给定一个Lattice $ \mathcal{L} $，与一个随机点$ \mathbf{t} $还有搜索距离$ d $，并且假设$ \mu(\mathbf{t}, \mathcal{L}) \le d $，CVP问题是让我们找到一个合理的格点$ \mathbf{Bx} \in \mathcal{L} $并且这个点到$ \mathbf{t} $的距离小于等于$ d $。

CVP问题对于搜索的范围和结果的大小已经有所约束了，但是并没有约束一共有多少结果和范围究竟有多大。所以CVP问题又可以细分为两种主要的版本。

BDD（Bounded Distance Decoding）问题

BDD问题规定了$ d < \lambda_1(\mathbf{L})/2 $，也就是说$ d $小于最短向量的一半。并且这个CVP问题最多只有一个唯一的解（at most 1 solution），并且这个解一定是距离$ \mathbf{t} $最近的格点。

ADD（Absolute Distance Decoding）问题

ADD问题则不同，规定了$ d \ge \mu(\mathbf{L}) $，也就是说$ d $大于整个格的覆盖半径了。这个时候，这个CVP问题至少会有一个解（at least 1 solution），但是我们找到的解并不一定是距离$ \mathbf{t} $最近的格点。

Lattice难题之间的相互联系

我们之前提到的SVP，CVP，以及CVP下面的BDD，ADD，都是公认的很难在多项式时间内有效解决的难题。我们来看一看这些难题之间的关联性。

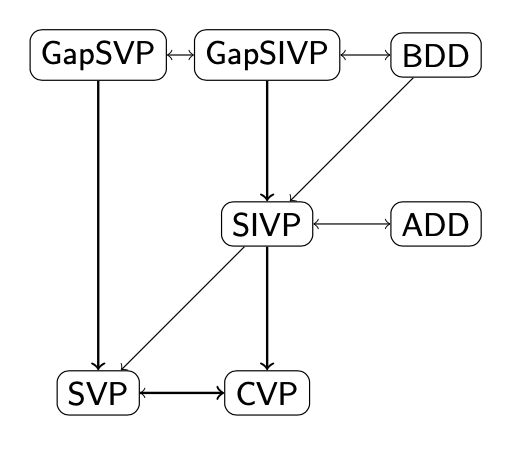
最近的二三十年来的各种paper逐渐的把这些难度的关系给证明了出来。具体的后面再详细研究。

ADD问题规约到SIVP问题上

上一部分的图中，我们发现ADD和SIVP问题被归为同一层（困难度）。这是因为经过一系列的变换，我们可以把ADD问题规约到SIVP问题上。

假设我们需要求解$ ADD(\mathcal{L}, \mathbf{t}) $，我们可以首先用SIVP算法得到这个Lattice的$ n $个独立最短向量$ \mathbf{V} = SIVP(\mathcal{L}) $。一旦得到了$ \mathbf{V} $之后，我们就可以选取这些向量作为基，平分整个多维空间$ \mathbb{R}^n $。然后我们只需要看$ \mathbf{t} $在那个分区中，然后向上或者向下取整一下，找到那个分区对应的格点，就是我们ADD问题的解了。

因为我们是使用了取整的操作来找到格点的，所以这个解的格点到$ \mathbf{t} $的距离，我们也可以找到一个最大的上限，即： $$ \sum_i \frac{1}{2} \lvert \lvert \mathbf{v}_i \rvert \rvert \le (n/2)\lambda_n \le n \mu$$

Lattice的几何构造

分析Lattice问题的时候，几何结构是一个非常强有力的工具。

举个例子，在最简单的笛卡尔坐标系整数格$ \mathbb{Z}^n $中，CVP问题是非常简单的。给定任意一个点$ \mathbf{t} $，$ CVP(\Lambda, \mathbf{t}) = \lfloor \mathbf{t} \rceil $。这也就是说我们只需要通过上下取整，就可以非常快速的的解决$ \mathbb{Z}^n $中的CVP问题。

为什么$ \mathbb{Z}^n $这么好解呢？这是因为$ \mathbb{Z}^n $中的基向量都是相互垂直的（orthogonal basis）。这也就是说，如果我们可以把一个任意的Lattice $ \Lambda $转换为一个垂直基的格，那么就可以非常轻松的的解决CVP了。

我们对把一个Lattice的基进行变换，找到一组非常接近垂直的基的过程，称之为Lattice Basis Reduction。这一过程在LLL82这一篇中有详细的描述。

Gram-Schmidt正交化

一个比较常见的Basis Reduction方法是Gram-Schmidt正交化过程。假设我们拥有一个格的基$ \mathbf{B} = [ \mathbf{b_1, \dots, b_n}] $。

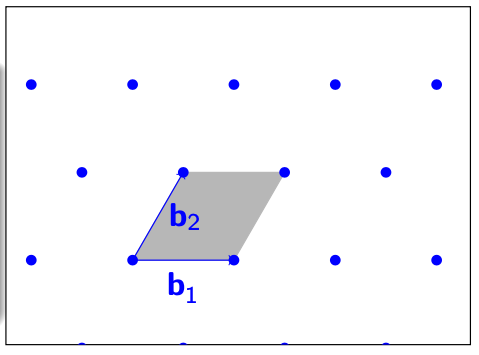
在这个Lattice中，我们发现这两个基向量是不垂直的。接下来，我们尝试找到一组互相垂直的基$ \mathbf{B^} $。 $$ \begin{align} \mathbf{b}_i^* &\in \mathbf{b}_i + [\mathbf{b}1, \dots, \mathbf{b}{i-1}]\mathbb{R}^{i-1}\ \mathbf{b}_i^* &\perp \mathbf{b}1, \dots, \mathbf{b}{i-1} \end{align*}$$ 在图中的这个案例中，一共有两个基向量，即$ \mathbf{b}_1, \mathbf{b}_2 $。我们首先根据以上等式，得到了第一个垂直基$ \mathbf{b}_1^* = \mathbf{b}_1 $。

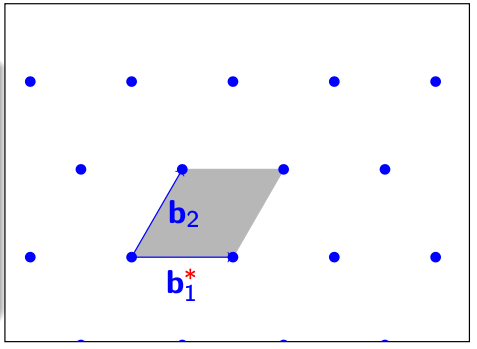
确定了$ \mathbf{b}_1^* $之后，我们可以计算第二个基$ \mathbf{b}_2^* $。因为$ \mathbf{b}_2^* $就是原本的$ \mathbf{b}_2 $再加上$ \mathbf{b}_1 $的任意线性组合，我们可以把这个取值范围用一条线来表示。

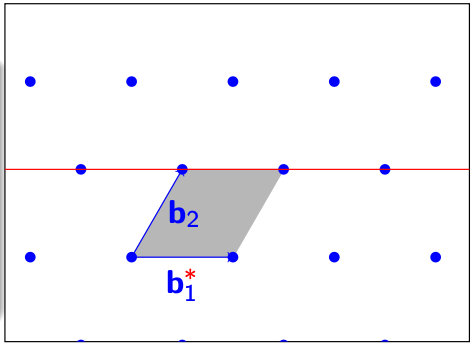
随后，我们可以选取在这一条线上符合条件的一个向量作为$ \mathbf{b}_2^* $，即与$ \mathbf{b}_1^* $垂直。

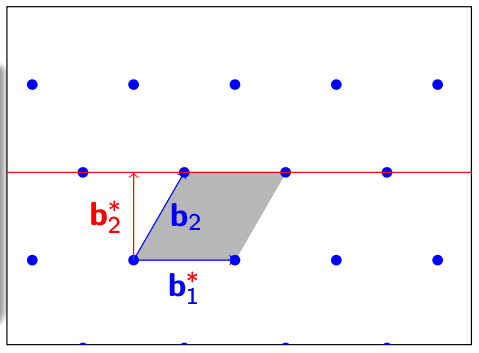
这样一来，我们就得到了一组新的相互垂直的基$ \mathbf{B^} $。仔细观察，我们会发现新的基向量并不在原本的Lattice内，所以$ \mathbf{B^} $并不是原本的格$ \mathbf{B}\mathbb{Z}^n $的基。但是值得注意的是，新的这组基组成的Determinant覆盖的空间（长方形），和原本的Lattice的基$ \mathbf{B} $的Determinant覆盖的（平行四边形）的大小是一样的。我们可以一组等式约束一下这个原有的Lattice $ \Lambda $： $$ det(\Lambda) = \prod_i \lvert \lvert \mathbf{b}_i^* \rvert \rvert \le \prod_i \lvert \lvert \mathbf{b}_i \rvert \vert$$

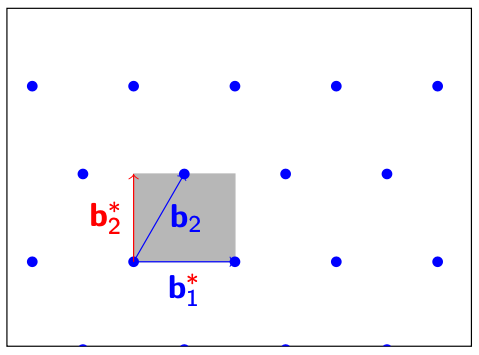
Lattice Rounding（取整）问题

之前说过，如果一个Lattice的基向量是互相垂直的（orthogonal），那么在这个Lattice中解决CVP问题是非常简单的。我们只需要根据这个点$ \mathbf{t} $的位置，向上或者向下取整，就可以找到最近的格点了。

对于没有垂直基的Lattice，比如说我们这里看到的$ \mathbf{B} $，我们可以通过Gram-Schmidt正交化的方法，找到一组拥有相同Determinant的垂直基$ \mathbf{B^*} $。

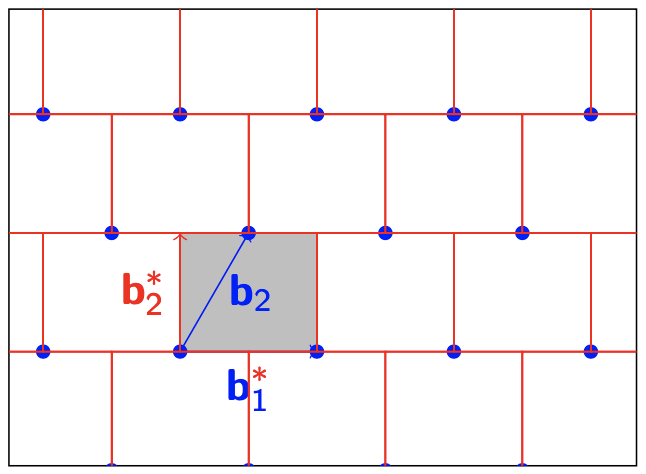
我们可以用这组垂直基$ \mathbf{B^*} $构成的Determinant空间来平分整个空间$ \mathbb{R}^n $。然后我们可以稍微的平移一下平分的空间，使得原本的Lattice $ \Lambda $的点都在长方形的中央。

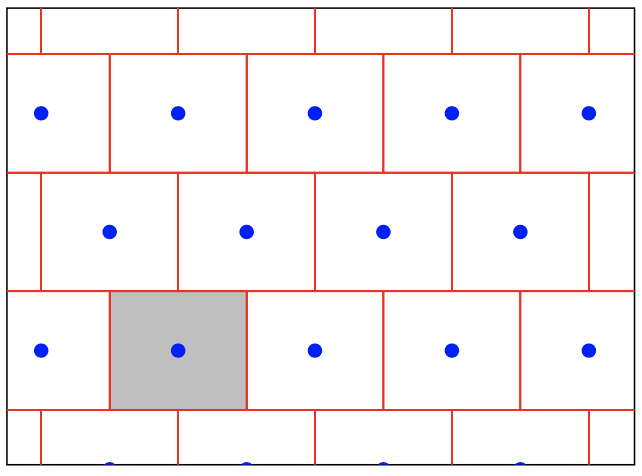
这样一来，我们可以把任意的一个点$ \mathbf{t} $取整到原本的Lattice中的一个点$ \mathbf{v} \in \Lambda $上来。因为我们是在做向上或者向下取整的操作，所以$ \mathbf{t, v} $这两个点上的距离不能超过长方体对角线长度的一半。 $$ \lvert \lvert \mathbf{t - v} \rvert \rvert \le \frac{1}{2} \sqrt{\sum_i \lvert \lvert \mathbf{b}_i^* \rvert \rvert ^2}$$

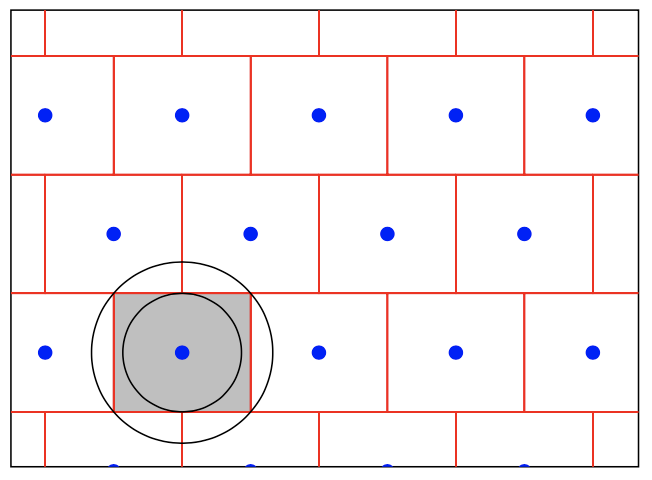
当我们做取整操作的时候，因为几何形状的原因，最后的得到的结果格点和CVP问题的真正解会略有误差。比如我们看上图，如果$ \mathbf{t} $的落点在内圈的这个小圆内，那么我们取整得到的一定会是CVP的正确解。如果用等式描述一下的话，那就是： $$ \lvert \lvert \mathbf{t - v} \rvert \rvert \le \min \lvert \lvert \mathbf{b}_i^* \rvert \rvert / 2$$ 只要满足这一条件，那么我们通过取整操作就能解决CVP。如果落点在外圈圆的话，那么很有可能就会被取整到隔壁的格点上去，那么那个点就不是最近的了。

Babai86提出了Nearest Plane Algorithm，这一算法正式的指出了取整方法可以逼近CVP问题的答案。这个算法说明了，我们Gram-Schmidt拿到的$ \mathbf{B^} $，可以找到一个在$ \sqrt{n} \cdot \frac{\max_i \lvert \vert \mathbf{b}_i^ \rvert \rvert}{\max_i \lvert \vert \mathbf{b}_i \rvert \rvert} $的误差范围内的CVP解。

Credits

The contents of this post is summarized from Prof. Daniele Micciancio’s lecture at Simon’s Institute Lattice Bootcamp.