初探全同态加密之三:构建GSW全同态加密系统
初探全同态加密之三:构建GSW全同态加密系统
上一期的文章中,我们一起了解了格密码学到底是什么,随后我们学习了LWE问题的构造。最后,我们把所学的内容组合起来,构成了格密码学中最经典的Regev加密算法。
希望看到这里,大家已经对上期讲到的内容已经有一个深刻的认知了。这一期,我们就可以真正开始实战最后的boss——开始构造全同态加密系统。
上期回顾
在开始之前,为了便于大家能够更好理解这期会描述的FHE系统,我们在此快速的复习一下之前两期文章讲到的比较关键的知识点。
LWE问题
上期文章中较为重点的内容就是LWE问题了。可以说正确的理解了LWE,格密码学和FHE问题就已经搞定了一大半了。
总结起来说,一个LWE的问题实例会随机生成一个比较大的矩阵$ A $,和一个不公开的私密向量$ s $。**搜索LWE问题(SLWE)**就是给定一个$ A $,以及带有误差的乘积$ (As + e) $,尝试还原出未知的向量$ s $。决策LWE问题(DLWE)就是分辨看到的一组矩阵与向量究竟是一个LWE实例$ (A, As + e) $,还是随机生成的矩阵$ (A, v \in \mathbb{Z}_q) $。一个合理构造的SLWE与DLWE问题在格密码学中都被定义为困难的问题。
为了更好的理解DLWE问题为什么是困难的,我们不妨看一下这张图。
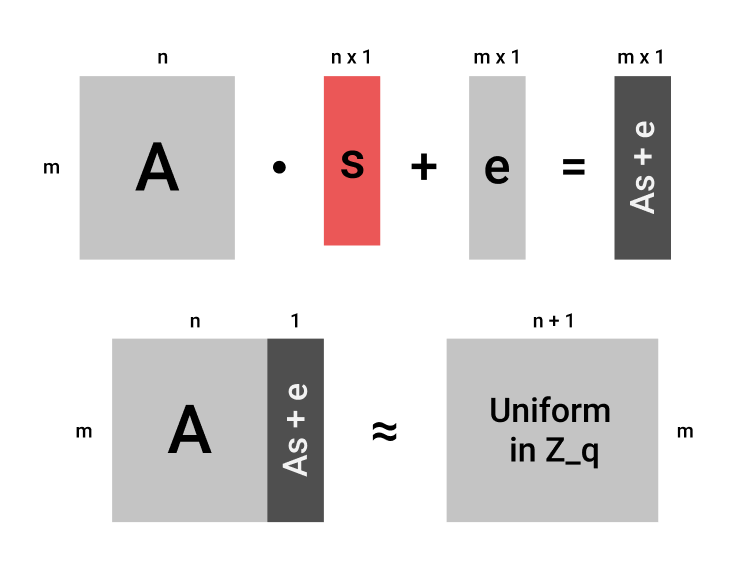
上面的图中,我们可以看到$ As + e $是通过矩阵相乘得到的。因为$ As + e $与$ A $都有$ m $行,所以我们可以把他们拼在一起,当作一个矩阵$ (A, As + e) $来看待。因为SLWE是困难的,所以我们无法从$ As + e $中有效的还原$ s $,这也就是说$ As + e $对于我们观察者来说,和随机的向量$ v $没有区别。这样一来,$ (A, As + e) $这么一个矩阵对于我们来说,和一个在$ \mathbb{Z}_q $中随机生成的$ m \times (n+1) $的矩阵也没有任何区别。
Regev加密算法与噪音区间
上期的最后,我们学习了Regev加密算法的构造。
简单的来说,Regev加密的精髓,就在于把一个bit的值(0或者1)映射到一个有限环形域(质数$ q $域)的两头。一般来说一头就是0,另一头是$ q/2 $。然后我们基于这个映射的基础上,生成一组LWE问题的实例$ As + e $,然后叠加到我们映射之后的原文上。
因为DLWE假设,所以$ As + e $可以被视作是一个随机生成的向量$ v \in \mathbb{Z}_q^m $,这也就是说我们等于是在原文的基础上叠加了一个随机值。这种一次性叠加随机值的加密方式,被称之为One-Time Pad(OTP)。对密码学比较了解的朋友们就会知道,OTP是**信息安全(Information Theoretic Secure)**的。这也就是为什么Regev加密之后的密文是语义安全的,因为原文加上随机值,看起来还是随机值。
在解密的时候,因为我们已经知道了未知向量$ s $的值,我们可以很简单的从密文中移除$ As $的部分,剩下一个噪音部分$ e $。所以最后我们得到的原文就是$ r^T \cdot e + q/2 \cdot x $。因为噪音$ e $在一个比较小的区间中,这不会影响到我们最后求解$ x $的值。
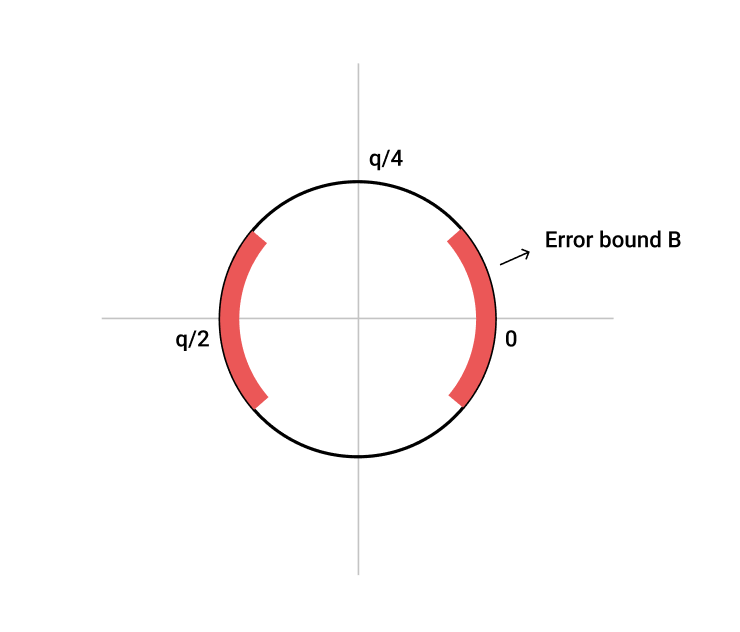
上面的图例很好的描述了Regev解密之后得到的原文在有限环状域上的映射。因为噪音的上限较小,所以我们得到的结果还是会在环的两侧。我们只需要看在哪一侧就知道原文是0还是1了。
如果噪音变大了,那么就有可能会导致误差的上限大于临界值,即$ q/4 $。一旦超过了临界值,那么0与1可能会被映射到相同的点上去,解密就有可能失败。这也就是为什么我们在Regev的定义中要求了$ q/4 > mB $这一限制。
全同态加密体系
最后,我们一起来回顾一下上上期讲到的,一个完整的全同态加密(FHE)体系的构造。
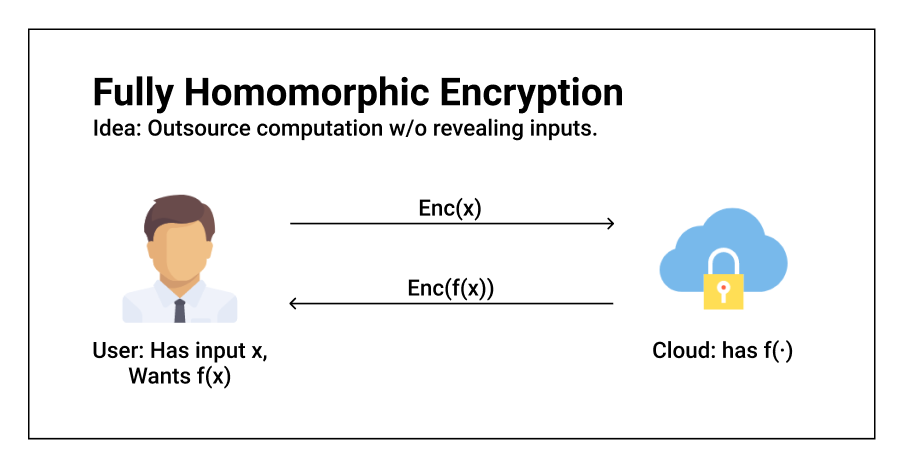
一个完整的FHE系统拥有以下四个基本算法:
- $ KeyGen(1^\lambda) \rightarrow sk $:KeyGen即密钥生成算法,将会生成其他FHE算法将要使用的密钥。
- $ Enc(sk, \mu \in {0,1}) \rightarrow ct $:加密算法$ Enc $可以加密用户的输入$ \mu $,输出密文$ ct $。
- $ Dec(sk, \mu \in {0, 1}) \rightarrow \mu $:解密算法$ Dec $可以把密文$ ct $还原为原来的$ \mu $。
- $ Eval(F, ct_1, …, ct_l) \rightarrow \tilde{ct} $:运算算法$ Eval $可以基于输入的$ l $个密文,进行任意功能$ F $的运算,最后得到加密后的结果$ \hat{ct} $。
与此同时,FHE系统还需要满足三大属性(properties):
- 正确性(Correctness):一个FHE系统必须要是正确的。具体来说,也就是加密之后的密文可以被成功解密,并且$ Eval $运算输出的密文也可以成功解密回原文。
- 语义安全(Semantic Security):FHE系统输出的密文必须要难以分辨。具体来说,如果有一个网络窃听者看到了所有的密文,那么这个窃听者并不能分辨出哪个密文是对应哪个原文的。
- 简短性(Compactness):FHE的运算算法$ Eval $输出的密文的长度一定要独立于功能$ F $的所对应的电路的大小。这一属性代表就算运算功能复杂,输出的密文仍然在一个可以控制的长度范围内,确保了FHE系统的实用性。
简单来说,FHE要解决的问题是这样的。假设一个用户拥有一个私密的值$ x $,但是他想要委托远程的服务器在不知晓$ x $的情况下计算一个功能$ f(x) $的值。
基于我们定义的四个算法,首先用户需要使用FHE加密算法来加密他的私密输入,得到$ Enc(s) $,然后发送给云端。随后,云端将会使用运算算法$ Eval $来计算得到$ Enc(F(x)) $,并返回给用户。最后用户使用FHE的密钥来解开密文,得到$ f(x) $。
FHE的四个阶段
我们在第一期的文章中,还学习了构成FHE系统的四个不同阶段:
- 部分同态(Partially Homomorphic Encryption):在这一阶段下,我们可以运算的功能$ F $只能够要么由加法/线性组合,要么由乘法构成。常见的例子有RSA(乘法同态)以及ElGamal(加法同态)。
- 近似同态(Somewhat Homomorphic Encryption):这一阶段的算法拥有不完整的同态属性,比如拥有Pairing配对的ElGamal循环群,具有完整的加法同态属性,但是只有非常薄弱的乘法同态属性。
- 有限级数全同态(Leveled Fully Homomorphic Encryption):这一阶段的算法可以同态运算任意形式的功能$ F $,但是功能$ F $所转换成的电路的复杂度不能超过上限$ L $,不然就会噪音太大丢失信息。
- 全同态(Fully Homomorphic Encryption):最后的阶段就是我们想要得到的FHE了。在这一阶段我们可以计算任意复杂度的功能$ F $,并且噪音可以被完美的控制在可控范围内。
我们之前还提到了,通过Bootstrapping的方式,可以有效的将一个有限级数全同态(LFHE)的系统转换为一个全同态(FHE)的系统。Bootstrapping这一概念是FHE界的开山鼻祖Craig Gentry在09年的PhD毕业论文中指出的。我们这次要讲到的GSW系统,就是一个FLHE系统,随后通过Bootstrapping被有效的转换为FHE系统。
综上所述,我们这一期来仔细的探讨一下,GSW中提出的LFHE系统是怎么构造的吧~
PS:这一段回顾的内容仅仅是前两期描述的一小部分。所以如果大家看到这里对FHE的定义与LWE问题还是不够了解的话,不妨再回去看看之前的文章,然后再回来继续往下看。
构造GSW-LFHE系统的三次尝试
GSW系统是Gentry,Sahai,Waters三位大牛在2013年提出的第三代同态加密系统。整套加密系统围绕了一个核心概念:矩阵的近似特征向量。
乍一听,这个概念有点云里雾里的。所以整篇论文其实也分了三个阶段,循序渐进的来介绍这一系统的构造。这三个阶段中,每一个阶段都提出了一个LFHE系统的尝试,并且评估了这一尝试是否可行。
话不多说,我们这一期就来详细的学习一下Gentry在原文中对于LFHE构造的三次尝试,并且逐步的推导出最后GSW系统的全貌吧。
第一次尝试:矩阵的特征值与特征向量
从FHE的定义来看,只要我们能够构建一个加密体系,并且可以保证$ Eval $算法可以任意计算加法与乘法,那么这个体系就是全同态的。
在线性代数中,一个矩阵的特征值与特征向量可以形成非常巧妙的线性关系。如果矩阵$ A $拥有特征向量$ x $,并且拥有对应的特征值$ \lambda $,那么以下关系成立: $$ Ax = \lambda x$$ 我们对于FHE系统的第一次尝试就基于这一特性。下面我们来看一看具体构造。
密钥生成KeyGen
密钥生成$ KeyGen $算法很简单,我们只需要随机选取一个向量$ \vec{s} $,然后作为我们加密的密钥。
“加密”算法Enc
$ Enc(\vec{s}, \mu) \rightarrow C $:如果我们要加密任意一个数字$ \mu $,我们只需要找到一个矩阵$ C $,使得$ C $满足: $$ C \cdot \vec{s} = \mu \cdot \vec{s}$$ 我们可以发现,这个等式中,$ \vec{s} $就是$ C $这个矩阵的特征向量(eigenvector),而我们加密的数字$ \mu $就是这个矩阵的一个**特征值(eigenvalue)**了。因为特征值可以是任何数字,所以我们这个“加密体系”可以加密任何有限域$ \mathbb{Z}_q $中的数字。
换句话来说,这个”加密“的过程中,我们只需要找到满足这一要求的矩阵$ C $,即拥有$ \vec{s} $以及$ \mu $这两个特征向量、特征值,然后再输出$ C $就是我们的密文了。
解密算法Dec
$ Dec(\vec{s}, C) $:如果需要解密一个密文矩阵$ C $的话,我们只需要把$ C $乘以我们的密钥$ \vec{s} $,就会得到$ \mu \cdot \vec{s} $了。然后我们观察结果向量的值,就可以推算出$ \mu $的值是什么,非常简单。
运算算法Eval
接下来,最重要的就是运算算法$ Eval $了。在上文的讨论中,我们知道一个体系只要可以运算加法以及乘法,那么这个体系就是全同态的。
接下来,我们看一看这个体系能否完成对于这两个功能的运算。假设我们拥有两个密文$ C_1, C_2 $对应原文$ \mu_1, \mu_2 $。
$ Eval(+, C_1, C_2) $:如果要运算加法的话,我们只需要把两个密文相加,输出$ \tilde{C} \leftarrow C_1 + C_2 $就可以了。这一结果的正确性很好验证,我们只要在运算结果上进行解密: $$ (C_1 + C_2) \cdot \vec{s} = C_1 \cdot \vec{s} + C_2 \cdot \vec{s} = \mu_1 \cdot \vec{s} + \mu_2 \cdot \vec{s} = (\mu_1 + \mu_2) \cdot \vec{s}$$ 解密的结果恰巧就是两个原文$ \mu_1, \mu_2 $相加的结果。
$ Eval(\times, C_1, C_2) $:运算乘法也非常简单,我们只需要把密文相乘,输出$ \tilde{C} \leftarrow C_1 \cdot C_2 $。这一结果的正确性也很容易验证: $$ (C_1 \cdot C_2) \cdot \vec{s} = C_1 \cdot (C_2 \cdot \vec{s}) = C_1 \cdot \mu_2 \cdot \vec{s} = \mu_2 \cdot C_1 \cdot \vec{s} = \mu_2 \cdot \mu_1 \cdot \vec{s} = (\mu_1 \cdot \mu_2) \cdot \vec{s}$$ 我们观察发现,这一加密体系似乎非常完美的保留了加法与乘法的同态性,而且一点噪音都没有!
“加密算法”的问题
我们的第一次尝试就完美的实现了全同态的所有要求,似乎看上去可以直接收摊,结束这篇文章了。
但是我们不能高兴的太早,因为这一体系有一个非常致命的弱点。如果细心的读者朋友们会发现,我们在讲述第一种方案的时候,一直给**“加密”**二字打上了引号。
这是因为,如果我们仔细观察这种体系生成的密文$ C $的话,我们会发现,$ C $就是一个正常的矩阵。我们只需要通过线性代数的方法,可以很简单的找到$ C $的特征向量与对应的特征值,然后就可以轻松的破解这个加密体系,根本不需要什么密钥$ \vec{s} $。我们甚至只需要用上一期讲到的高斯消除法,就可以简单的得到$ \vec{s} $与$ \mu $这两个值。这也就是说,我们的第一种FHE体系,只有全同态(FH)并没有加密(E),所有的隐私内容还是原封不动的暴露在外面。
但是这一架构对于我们后续的尝试是一个很好的启发,我们缺哪里补哪里就行了。上一期的文章中,我们讲到高斯消除法可以很好的找到线性方程组的解,但是如果我们叠加了一个噪音的话,就变成了困难的LWE问题。我们这里不妨也做同样的尝试,在特征向量与特征值的等式中加入噪音,看看会不会有所变化。
第二次尝试:加入随机噪音
这一次,我们尝试像LWE一样,在原本体系中引入随机噪音,看看会有什么结果。总的来说,我们可以尝试把原本的特征向量等式转换为: $$ C \cdot \vec{s} = \mu \cdot \vec{s} + \vec{e}$$ 这样一来,就等于在原有的等式中加入了一个随机噪音向量$ \vec{e} $。我们系统性的定义一下这一体系的具体构造。
密钥生成KeyGen
$ KeyGen(1^\lambda) $:我们更加全面的定义一下密钥生成。首先,我们随机生成一个私密向量$ \tilde{s} \in \mathbb{Z}_q^{n-1} $,然后我们再这个向量的最下面再加上一个$ -1 $,构成我们的密钥向量$ \vec{s} \leftarrow \begin{pmatrix}\tilde{s}\-1\end{pmatrix} $。最后我们输出$ \vec{s} \in \mathbb{Z}_q^n $作为我们的密钥。
加密算法Enc
$ Enc(\vec{s}, \mu \in \mathbb{Z}_q) $:如果要加密任意一个$ \mathbb{Z}_q $内的数字$ \mu $的话,我们取得密钥$ \vec{s} $的前$ n-1 $项,还原出随机生成的$ \tilde{s} $。然后我们需要基于$ \tilde{s} $构建一个LWE问题实例。
首先,我们随机生成一个矩阵$ A \stackrel{R}{\leftarrow} \mathbb{Z}q^{n \times (n-1)} $与对应的随机噪音向量$ \vec{e} \stackrel{R}{\leftarrow} x_B^n $,然后我们生成最后的密文$ C $: $$ C = \underbrace{(A, A \cdot \tilde{s} + \vec{e})}\text{LWE Instance} + \overbrace{\mu \cdot I_n}^\text{message} \in \mathbb{Z}_q^{n \times n}$$ 这里等式中的$ I_n $是一个$ n \times n $阶的单位矩阵。
观察这个加密算法我们可以发现,在这里我们把LWE的问题实例($ A, A \cdot \tilde{s} + e $)拼接起来变成一个$ n \times n $的矩阵,然后叠加在我们想要加密的信息$ \mu \cdot I_n $上面。因为DLWE假设,我们可以把这一过程看作是一个One-Time Pad,即叠加了一个随机值的过程。这样一来,就可以确保密文是安全的。
解密算法Dec
$ Dec(\vec{s}, C) $:如果我们需要解密一个密文矩阵$ C $的话,我们只需要计算$ C \cdot \vec{s} $,然后观察得到的结果大约是$ \vec{s} $的几倍,就可以还原出我们的原文$ \mu $了。
这一解密算法的正确性(Correctness)很好理解,我们只需要展开$ C \cdot \vec{s} $这一表达式: $$ \begin{align} C \cdot \vec{s} &= ((A, A \cdot \tilde{s} + \vec{e}) + \mu \cdot I_n) \cdot \vec{s}\ &= (A, A \cdot \tilde{s} + \vec{e}) \cdot \vec{s} + \mu \cdot I_n \cdot \vec{s}\ &= A \cdot \tilde{s} - (A \cdot \tilde{s} + \vec{e}) + \mu \cdot \vec{s}\ &= \mu \cdot \vec{s} - \vec{e} \end{align}$$ 因为我们的解密密钥$ \vec{s} $就是原本的LWE未知向量$ \tilde{s} $再最后多加了一项$ -1 $,所以我们计算矩阵相乘的时候,就等于是把LWE的问题矩阵$ A $与未知向量$ \tilde{s} $相乘,再减去$ A \cdot \tilde{s} + \vec{e} $,最后就只剩一项噪音向量**。
观察解密结果我们可以发现,我们最后得到的关系$ C \cdot \vec{s} = \mu \cdot \vec{s} \pm \vec{e} $,和我们一开始提出的在特征向量等式中加入噪音是一样的了。还有一点需要注意的是,因为我们在LWE问题中定义的噪音只是绝对值需要符合一个上限$ B $,所以这里噪音向量的正负$ \pm $没有任何区别。
因为这里解密得到的关系式和之前的特征向量关系式大概一致,我们可以称这里的私密向量$ \tilde{s} $为矩阵$ C $的近似特征向量(approximate eigenvector)。
运算算法Eval
接下来就是重头戏了。当我们加入了随机噪音,确保了体系的安全性之后,之前的全同态属性能否维持呢?我们接下来详细的看一下。
$ Eval(+, C_1, C_2) \rightarrow C_1 + C_2 $:计算密文之间的加法和我们第一次尝试的构造相同——我们只需要把两个密文加起来就可以了。为了证明正确性,我们同样尝试对运算结果进行解密: $$ \begin{align*} (C_1 + C_2) \cdot \vec{s} &= C_1 \cdot \vec{s} + C_2 \cdot \vec{s}\ &= \mu_1 \cdot \vec{s} + \vec{e}_1 + \mu_2 \cdot \vec{s} + \vec{e}_2\ &= (\mu_1 + \mu_2) \cdot \vec{s} + \underbrace{(\vec{e}_1 + \vec{e}2)}\text{small error term} \end{align*}$$ 把表达式展开之后,我们发现我们把$ C_1 $和$ C_2 $相加之后,就可以非常有效的得到$ \mu_1 + \mu_2 $的密文。但是相对应的,这两个密文中所带的随机噪音$ \vec{e}_1, \vec{e}_2 $也会被叠加起来。但是所幸我们规定的噪音取值上限$ B $一般来说比较小,所以就算两个叠加起来,我们最多也是到$ 2B $的容错率。考虑到$ B « q $的情况下,我们仍然可以把得到的$ \vec{e}_1 + \vec{e}_2 $看作一个可以接受的噪音值。
$ Eval(\times, C_1, C_2) \rightarrow C_1 \cdot C_2 $:计算乘法和上个方案也是相似的,我们只需要把两个密文相乘,就可以得到结果了。接下来,我们把相乘的结果解密的过程展开: $$ \begin{align*} (C_1 \cdot C_2) \cdot \vec{s} &= C_1 \cdot (C_2 \cdot \vec{s})\ &= C_1 \cdot (\mu_2 \cdot \vec{s} + \vec{e}_2)\ &= \mu_2 \cdot C_1 \cdot \vec{s} + C_1 \cdot \vec{e}2\ &= \underbrace{\mu_1 \cdot \mu_2 \cdot \vec{s}}\text{Result} + \underbrace{\mu_2 \cdot \vec{e}1}\text{ok error term} + \underbrace{C_1 \cdot \vec{e}2}\text{large error term!} \end{align*}$$ 观察展开的表达式,我们可以发现解密之后的结果分为三项,分别为我们想要得到的乘法同态加密结果$ \mu_1 \cdot \mu_2 \cdot \vec{s} $,和两个和随机噪音有关的噪音向量$ \mu_2 \cdot \vec{e}_1 $以及$ C_1 \cdot \vec{e}_2 $。
我们得到的结果中,第一项是我们想要的结果,自然是极好的。我们重点需要观察一下后面两项的大小以及取值上限。
第一项噪音即$ \mu_2 \cdot \vec{e}_1 $,由于噪音向量$ \vec{e} $的取值绝对值上限为$ B $,那么这一项的取值上限即$ \mu \cdot B $。为了使得这一项的噪音不会过大,有一个很简单的方法:我们规定一次只能加密一个bit,这样$ \mu $的取值范围就在$ {0, 1} $之内。这样一来,我们这一项的噪音取值上限仍然还是$ B $。
然而第二项噪音$ C_1 \cdot \vec{e}_2 $就没有那么简单了。因为$ C_1 $是一个随机取值于$ \mathbb{Z}_q $的随机矩阵,这也就是说**$ C_1 $每个值的最大上限会有$ q/2 $这么大**。这样一来,就算$ \vec{e}_2 $的取值范围很小,这一项的乘积也会特别大,直接撑爆我们的噪音上限$ q/4 $,导致整个密文失效,不能被解密。
噪音过大的问题
虽然在原有的特征向量系统中加入噪音可以有效的使整个FHE系统变得安全,但是与此同时也使得整个FHE系统丢失了原本的全同态特性——因为运算乘法的时候会引入过大的噪音,导致运算结果无法被成功解密。
我们观察运算乘法之后的解密结果之后,发现一共有两项噪音。第一项较小,可以通过约束$ \mu $的取值来约束这一项的取值上限。然而第二项噪音是没有上限的(unbounded),因为就算噪音向量$ \vec{e} $拥有上限$ B $,矩阵$ C $中的数字是毫无约束的随机数,在$ \mathbb{Z}_q $中任意取值。
看似这套系统哪里都没问题,唯独在运算乘法同态的时候出现了一些令人不满意的瑕疵。但是我们不能就此放弃,只要缺哪里补哪里就行了。
我们观察到最后一项$ C_1 \cdot \vec{e}_2 $取值没有上限的原因是因为矩阵$ C_1 $是在$ \mathbb{Z}q $中任意取值的。这么说矩阵$ C $的**无限范数(infinity norm)**就是$ \mid\mid C \mid\mid\infty \le q/2 $。那么有没有什么办法,可以让我们使得$ C $的无限范数下降到一个可控的小范围内,但是仍然保证$ C $矩阵中的数字是随机取的呢?
答案其实很简单,我们需要借助一个小工具:二进制分解。
二进制分解(Binary Decomposition)
如果我们拥有一个数字$ x \in \mathbb{Z}q $,那么我们可以把这个数字用二进制的一串bits表达,使得这个数字的范数(norm)降低。我们定义$ \hat{x} $为$ x $的二进制分解态: $$ \hat{x} = (x_0, x_1, \dots, x{log(q)-1}) \in {0, 1}^{log(q)}$$ 当我们分解$ x \in \mathbb{Z}q $为二进制的时候,我们最多会得到$ log(q) $个bit,然后每个bit都在$ {0, 1} $的区间范围内。这样一来,如果我们观察$ \hat{x} $的无限范数的话,我们会发现: $$ \mid\mid \hat{x} \mid\mid\infty \le 1$$ 这样一来,我们就可以有效的把一个大的数字转换为由一串小数表达的形式。
同理可得,我们也可以对于一个向量$ v $进行二进制分解,得到$ \hat{v} $。具体操作的方法其实很简单,我们只需要对这个向量中的每一个元素分别进行二进制分解,然后连在一起就可以了。假如我们拥有$ v = (v_0, v_1, \dots, v_{n-1}) $: $$ \hat{v} = (\underbrace{v_{0,0}, \dots, v_{0, log(q)-1}}\text{log(q)-1 elements}, v{1, 0}, \dots, v_{1, log(q)-1}, \dots, v_{n-1, 0}, \dots, v_{n-1, log(q)-1})$$ 分解得到的$ \hat{v} $一共会拥有$ n \times log(q) $个元素,而每个元素都是一个二进制bit。
我们如果再扩展延伸一下这个概念,甚至也可以对一个矩阵$ C $进行二进制分解。操作的方法也一样,我们把这个矩阵的每一行都作为一个单独的向量进行二进制分解即可。假如我们拥有一个$ m \times n $的矩阵$ C $: $$ C = \begin{pmatrix}C_0\\vdots\C_{m-1}\end{pmatrix} \rightarrow\hat{C} = \begin{pmatrix}\hat{C_0}\\vdots\\hat{C_{m-1}}\end{pmatrix}$$ 最后我们得到的$ \hat{C} $的维度就是$ m \times n \cdot log(p) $了,非常简单。
二进制分解另外一个好处是,如果我们想要把二进制分解态的$ \hat{x} $还原回原来的数字$ x $的话,整个还原的过程可以被描述为一个线性变换的过程。假如我们有$ \hat{x} = (x_0, \dots, x_{log(q)-1}) $,我们可以这样还原$ x $: $$ x = \sum_{i=0}^{log(q)-1} x_i \cdot 2^i$$ 同理,我们还原一个二进制分解的矩阵$ \hat{C} $的过程也是一个线性变换的过程。我们可以用矩阵的形式来表达这一线性变换。假设我们拥有二进制分解态的矩阵$ \hat{C} $,那么可以通过一个二进制重组矩阵$ G $变换重组到$ C $: $$ \begin{align*} C &= \hat{C} \cdot G\ &=\begin{bmatrix} \hat{C_1}\ \vdots\ \hat{C_m} \end{bmatrix} \cdot G \ &=\begin{bmatrix} C_{0,0,0}&\cdots&C_{0,0,log(q)-1}&\cdots&C_{0,n-1,0}&\cdots&C_{0,n-1,log(q)-1}\ \vdots&\ddots&\vdots&\ddots&\vdots&\ddots&\vdots\ C_{m-1,0,0}&\dots&C_{m-1,0,log(q)-1}&\dots&C_{m-1,n-1,0}&\dots&C_{m-1,n-1,log(q)-1} \end{bmatrix} \cdot G \end{align*}$$ 因为我们要确保$ \hat{C} $展开的每$ log(q) $项都可以被重新被二进制重组为所对应的值,我们的重组矩阵$ G $大致如下: $$ G = \begin{bmatrix} 2^0&0&\cdots&0\ 2^1&0&\cdots&0\ \vdots&\vdots&\ddots&\vdots\ 2^{log(q)-1}&0&\cdots&0\ 0&2^0&\cdots&0\ \vdots&\vdots&\ddots&\vdots\ 0&0&\cdots&2^{log(q)-1} \end{bmatrix}$$ 矩阵$ G $中,每一列的系数对应了$ \hat{C} $中的每一行的每$ log(q) $个bits的线性重组。这样一来,最后相乘就可以还原回我们初始的$ C $来。
划重点:这里比较重要的是,我们可以观察二进制重组矩阵$ G $的第一行为: $$ G_1 = \begin{bmatrix}1&0&\cdots&0\end{bmatrix}$$ 在$ G_1 $中,只有第一项是1,其余都是0。这一点之后会方便我们后续优化下一阶段的FHE系统的计算。
因为我们把二进制重组用矩阵$ G $来表示,所以我们往往也把二进制分解这一过程用$ G^{-1}(\cdot) $来表示,即$ \hat{C} = G^{-1}(C) $。
当我们掌握了二进制分解这个工具之后,让我们再回到我们的话题上,看看能否把它加入我们当前构造的不完美FHE体系中。
第三次尝试:加入二进制分解(GSW系统)
上一次尝试中,最后不完美的部分在于计算乘法运算的时候,我们会得到一个没有约束的噪音项$ C_1 \cdot \vec{e}_2 $。经过对于矩阵$ C $的观察之后,我们发现只要确保矩阵$ C $里面的值可以被约束在一个小的区间,那么整体来说这一个噪音项就不会带来太大的噪音上限。
刚才我们也学习了二进制分解可以很有效的把一个高范数的矩阵$ C $分解为一个低范数的二进制bit矩阵$ \hat{C} $,并且二进制重组的过程可以被完美的描述为一个线性变换(矩阵)。
现在,我们来看看怎么把二进制分解的概念加到我们的FHE系统中来。
话不多说,上定义。
密钥生成KeyGen
$ KeyGen(1^\lambda) $:密钥生成和我们之前的系统一样,我们随机选取一个向量$ \tilde{s} $,并且输出$ \vec{s} \leftarrow \begin{pmatrix}\tilde{s}\-1\end{pmatrix} $为密钥。
加密算法Enc
$ Enc(\hat{s}, \mu \in {0, 1}) $:因为上面讨论到了如果$ \mu $过大,会导致第一个噪音项$ \mu_2 \cdot \vec{e}_1 $过大,所以我们这里约束一下,每次只能加密一个二进制bit,即$ \mu \in {0,1} $。
加密的过程和之前大致相似,略有小的微调。首先,我们需要构造LWE问题实例。在定义LWE的各项系数的时候,为了使得维度相符,我们选择$ m = n \cdot log(q) $。然后我们选取随机矩阵$ A \stackrel{R}{\leftarrow} \mathbb{Z}_q^{m \times (n-1)} $,与噪音向量$ \vec{e} \stackrel{R}{\leftarrow} x_B^m $。最后,我们选取密钥$ \vec{s} $的前$ n-1 $项,得到$ \tilde{s} $,然后我们计算得到密文$ C $: $$ C = (A, A \cdot \tilde{s} + \vec{e}) + \mu \cdot G \in \mathbb{Z}_q^{m \times n}$$ 和之前不同的是,我们这里不用单位矩阵,而是使得$ \mu $乘以二进制重组矩阵$ G $。
当我们算出$ C $之后,我们不直接输出$ C $,而是输出$ C $的二进制分解态$ \hat{C} \leftarrow G^{-1}(C) $作为我们的密文。
解密算法Dec
$ Dec(\vec{s}, \hat{C}) $:解密的过程其实不难,由于我们之前输出了$ C $的二进制分解态$ \hat{C} $,我们需要首先对其进行二进制重组$ G $,然后再进行正常的解密。 $$ \begin{align*} \hat{C} \cdot G \cdot \vec{s} &= C \cdot \vec{s}\ &= (A, A \cdot \tilde{s} + \vec{e}) \begin{pmatrix}\tilde{s}\-1\end{pmatrix} + \mu \cdot G \cdot \vec{s}\ &= A \cdot \tilde{s} - A \cdot \tilde{s} - \vec{e} + \mu \cdot G \cdot \vec{s}\ &= \mu \cdot G \cdot \vec{s} - \vec{e} \end{align*}$$ 最后我们会得到一个$ m $个元素的向量作为结果的乘积,而这个向量中则蕴含了我们加密的原文$ \mu $的信息。
我们可以观察一下最后得到的表达式的第一项$ \mu \cdot G \cdot \vec{s} \in \mathbb{Z}_q^m $。因为我们前文介绍二进制分解的时候,发现矩阵$ G $的第一行是$ G_1 = \begin{bmatrix}1&0&\cdots&0\end{bmatrix} $,所以我们这一项得到的第一个元素是: $$ (\mu \cdot G \cdot \vec{s})_1 = \mu \cdot (\vec{G})1 \cdot \vec{s} = \mu \cdot \begin{bmatrix}1&0&\cdots&0\end{bmatrix} \cdot \begin{bmatrix}s_1\\vdots\s{n-1}\-1 \end{bmatrix} = \mu \cdot s_1$$ 因为$ s_1 $就是在密钥生成阶段随机选取的一个数字,我们知道$ s_1 $是随机分布于$ \mathbb{Z}_q $的,也就是说很大的几率上,$ s_1 $会是一个比较大的数字(远大于可以接受的噪音上限)。
这样一来,我们可以只计算、观察解密算法得到的结果向量的第一项,然后输出原文$ \mu $: $$ \text{output: } \begin{cases} 0, & \text{if } \mid\mid (\mu \cdot G \cdot \vec{s})_1 - \vec{e}_1 \mid\mid \text{ is small}\ 1, & \text{otherwise} \end{cases}$$ 如果结果较小(在可以接受的噪音范围之内,比如$ q/4 $),那么就输出$ \mu=0 $,反之输出$ \mu=1 $。
运算算法Eval
**我们拭目以待的部分终于到来了。**接下来我们来看看,大费周折了这么久,加上了各种酷炫机制的第三次尝试,到底能否通过FHE的考验。
加法同态和之前是一样的,如果我们要在两个密文$ \hat{C_1}, \hat{C_2} $上运算加法的话,我们只需要相加就可以了。验证也很简单: $$ \begin{align*} (\hat{C_1} + \hat{C_2}) \cdot G \cdot \vec{s} &= \hat{C_1} \cdot G \cdot \vec{s} + \hat{C_2} \cdot G \cdot \vec{s}\ &= \mu_1 \cdot G \cdot \vec{s} - \vec{e}_1 + \mu_2 \cdot G \cdot \vec{s} - \vec{e}2\ &= \underbrace{(\mu_1 + \mu_2) \cdot G \cdot \vec{s}}\text{addition of plaintext} - \underbrace{(\vec{e}_1 + \vec{e}2)}\text{small error term} \end{align*}$$ 我们最后得到的噪音仅仅是$ \hat{e}_1 + \hat{e}_2 $而已,这样的噪音增长对我们来说是非常好的。
乘法同态才是真正需要考验的重要环节。我们来看看,如果把两条密文相乘,最后得到的结果能否通过解密这一关: $$ \begin{align*} (\hat{C_1} \cdot \hat{C_2}) \cdot G \cdot \vec{s} &= \hat{C_1} \cdot (\hat{C}_2 \cdot G) \cdot \vec{s}\ &= \hat{C_1} \cdot C_2 \cdot \vec{s}\ &= \hat{C_1} \cdot (\mu_2 \cdot G \cdot \vec{s} + \vec{e}_2)\ &= \mu_2 \cdot \hat{C_1} \cdot G \cdot \vec{s} + \hat{C_1} \cdot \vec{e}_2\ &= \mu_2 \cdot (\mu_1 \cdot G \cdot \vec{s} + \vec{e}_1) + \hat{C_1} \cdot \vec{e}2\ &= \underbrace{(\mu_1 \cdot \mu_2) \cdot G \cdot \vec{s}}\text{multiplication of pt} + \underbrace{\mu_2 \cdot \vec{e}1}\text{small error term} + \underbrace{\hat{C_1} \cdot \vec{e}2}\text{relatively small} \end{align*}$$ 我们会发现,最后得到的结果和之前大致一样分三项。
第一项是我们真正需要的乘法同态运算的原文结果,我们抛开不看。第二项是我们之前讨论过的较小的噪音项,由于我们已经约束$ \mu $为一个二进制bit,所以这一项的噪音其实很小。
最重要的就是这里的第三项了。我们发现这里和$ \vec{e}_2 $相乘的$ \hat{C_1} $是一个二进制矩阵,所以$ \hat{C_1} $的无限范数非常小。这也就是说,这两个矩阵相乘最后的结果不会太大。假设在最坏的情况下(即$ \hat{C_1} $的每一项都为1),那么我们得到的最坏的噪音上限也**仅仅是$ n \cdot log(p) \times B $而已!**这比起我们之前的$ m \cdot p \times B $来说,已经好了太多了。
虽然说当$ n $或者$ p $大了之后,这一项噪音的大小也会随之上升,但是在一个可控的噪音上限下(比如$ q/4 $),我们已经可以做很多次加法和乘法了。我们可以用一个数字$ L $来量化一下一个噪音区间中可以进行的同态运算的次数。也就是说,当我们对于一个刚刚生成的低噪音的密文进行$ L+1 $次同态乘法运算之后,密文的噪音就会大过可以接受的上限,然后导致解密失败。
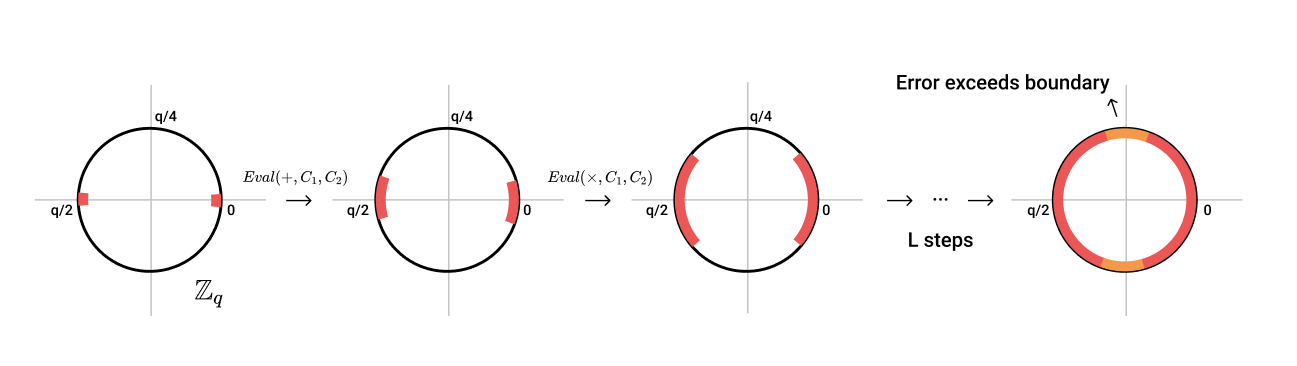
上面的图很好的表述了噪音增长的过程。在$ \mathbb{Z}_q $的环中,我们可以看到映射在两头的0和1的值的噪音区间不断增大,直到进行了$ L+1 $次同态计算之后,噪音的区间大过了一个半圆,导致1与0的界限消失了。
综上所述,我们成功的构造了一个可以让我们进行任意全同态运算(最多$ L $次乘法)的FHE系统!这就是GSW系统中描述的有限级数全同态加密(LFHE)系统的全貌啦。
篇尾小结
相比起前两篇文章来说,这一篇文章可以说是最学术、数学公式最多的了。我尽可能地在描述的过程中用大白话来讲述LFHE系统的构造。如果大家在看的过程中还有一些疑惑,不妨把有困惑的地方再读一遍,或者私信我一起交流!
我在文章开头有所提到:GSW系统的精华就在于近似特征向量这么一个定义。我们从普通的特征向量出发构建了一个全同态、但是不加密的系统;随后,我们加入了LWE问题中类似的噪音向量,构成了一个部分同态、但加密的系统。最后,我们使用二进制分解这么一个工具,构成了GSW中最后提到的有限级数全同态加密系统。
看到这儿,如果你已经能get到GSW系统在做什么,是怎么来的的话,**恭喜你已经掌握FHE系统构造的精髓啦!**这是一件值得高兴的事情,因为FHE是一个相对来说非常年轻(~10年)的领域,我们已经站在密码学技术很前沿了。
下一步,是什么?
我们现在已经根据GSW这一篇paper所述的,一起构建出了一套LFHE系统了。但是就像我在第一篇中承诺的——我们要再接再厉,冲向真正的FHE。
(注:GSW的paper中讲到的加密算法和我们本文中提到的可能有所出入,使用的是一种非对称的形式,而我们用的是对称加密形式。但是这并不会影响整个体系的正确性或者是功能性。个人觉得这样更好理解一点。)
为了能够把LFHE系统转换为真正的FHE系统,我们就需要用到Gentry大佬提出来的Bootstrapping这一方法了。简单的来说,Bootstrapping可以把一个即将达到临界值的、带有很大噪音的密文,”刷新“成一个噪音很小的密文,这样就可以无限制的进行同态运算了。
下一期,我们详细的介绍一下GSW系统中是如何应用Bootstrapping把原本的LFHE转换为FHE的。篇幅允许的话,我们还可以来探讨一下现有FHE库(如HELib,SEAL,TFHE)等的区别。下期见啦~